
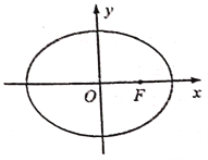
【题目】如图,在平面直角坐标系xOy中,椭圆C:![]() (a>b>0)经过点(0,
(a>b>0)经过点(0,![]() ),点F是椭圆的右焦点,点F到左顶点的距离和到右准线的距离相等.过点F的直线
),点F是椭圆的右焦点,点F到左顶点的距离和到右准线的距离相等.过点F的直线![]() 交椭圆于M,N两点.
交椭圆于M,N两点.
(1)求椭圆C的标准方程;
(2)当MF=2FN时,求直线![]() 的方程;
的方程;
(3)若直线![]() 上存在点P满足PM·PN=PF2,且点P在椭圆外,证明:点P在定直线上.
上存在点P满足PM·PN=PF2,且点P在椭圆外,证明:点P在定直线上.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析.
;(3)见解析.
【解析】
(1)由题意,b=![]() ,再由点F到左顶点的距离和到右准线的距离相等,得a+c=
,再由点F到左顶点的距离和到右准线的距离相等,得a+c=![]() ,结合隐含条件解得a=2,c=1,则椭圆方程可求;
,结合隐含条件解得a=2,c=1,则椭圆方程可求;
(2)当直线l与x轴重合时,求得MF=3NF,不合题意;当直线l与x轴不重合时,设直线l的方程为x=my+1,M(x1,y1),N(x2,y2),联立直线方程与椭圆方程,化为关于y的一元二次方程,由根与系数的关系及MF=2FN求得m值,则直线方程可求;
(3)当直线l的斜率为0时,设P(x0,y0),由PMPN=PF2,求得![]() ,当直线l的斜率不为0时,由(2)中的根与系数的关系及PMPN=PF2,求得
,当直线l的斜率不为0时,由(2)中的根与系数的关系及PMPN=PF2,求得![]() ,代入直线方程得
,代入直线方程得![]() ,由此可得点P在定直线
,由此可得点P在定直线![]() 上.
上.
(1)设椭圆的截距为2c,由题意,b=![]() ,
,
由点F到左顶点的距离和到右准线的距离相等,得a+c=![]() ,
,
又a2=b2+c2,联立解得a=2,c=1.
∴椭圆C的标准方程为![]() ;
;
(2)当直线l与x轴重合时,M(﹣2,0),N(2,0),此时MF=3NF,不合题意;
当直线l与x轴不重合时,设直线l的方程为x=my+1,M(x1,y1),N(x2,y2),
联立 ,得(3m2+4)y2+6my﹣9=0.△=36m2+36(m2+4)>0.
,得(3m2+4)y2+6my﹣9=0.△=36m2+36(m2+4)>0.
![]() ①,
①,![]() ②,由MF=2FN,得y1=﹣2y2③,
②,由MF=2FN,得y1=﹣2y2③,
联立①③得,![]() ,
,
代入②得, ,解得
,解得![]() .∴直线方程为
.∴直线方程为![]() ;
;
(3)当直线l的斜率为0时,则M(2,0),N(﹣2,0),设P(x0,y0),
则PMPN=|(x0﹣2)(x0+2)|,∵点P在椭圆外,∴x0﹣2,x0+2同号,
又![]() ,解得
,解得![]() .
.
当直线l的斜率不为0时,由(2)知,![]() ,
,
![]() .
.
∵点P在椭圆外,∴y1﹣y0,y2﹣y0同号,
∴PMPN=(1+m2)(y1﹣y0)(y2﹣y0)=![]()
![]() ,
,
整理得![]() ,代入直线方程得
,代入直线方程得![]() .∴点P在定直线
.∴点P在定直线![]() 上.
上.


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:高中数学 来源: 题型:
【题目】在平面上给定相异两点A,B,设P点在同一平面上且满足![]() ,当
,当![]() 且
且![]() 时,P点的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故我们称这个圆为阿波罗尼斯圆,现有双曲线
时,P点的轨迹是一个圆,这个轨迹最先由古希腊数学家阿波罗尼斯发现,故我们称这个圆为阿波罗尼斯圆,现有双曲线![]() (
(![]() ,
,![]() ),A,B为双曲线的左、右顶点,C,D为双曲线的虚轴端点,动点P满足
),A,B为双曲线的左、右顶点,C,D为双曲线的虚轴端点,动点P满足 ,
,![]() 面积的最大值为
面积的最大值为![]() ,
,![]() 面积的最小值为4,则双曲线的离心率为______.
面积的最小值为4,则双曲线的离心率为______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() (
(![]() )经过点
)经过点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 有两个不同的交点
有两个不同的交点![]() 、
、![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() ,直线
,直线![]() 交
交![]() 轴于
轴于![]() .
.
(1)若直线![]() 过点
过点![]() ,求直线
,求直线![]() 的斜率的取值范围;
的斜率的取值范围;
(2)若直线![]() 过点
过点![]() ,设
,设![]() ,
,![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)若直线![]() 过抛物线
过抛物线![]() 的焦点
的焦点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数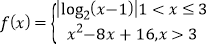 若方程f(x)=m有4个不同的实根x1,x2,x3,x4,且x1<x2<x3<x4,则(
若方程f(x)=m有4个不同的实根x1,x2,x3,x4,且x1<x2<x3<x4,则(![]() )(x3+x4)=( )
)(x3+x4)=( )
A. 6 B. 7 C. 8 D. 9
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的右焦点为
的右焦点为![]() ,
,![]() 是椭圆
是椭圆![]() 上一点,
上一点,![]() 轴,
轴,![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 、
、![]() 两点,线段
两点,线段![]() 的中点为
的中点为![]() ,
,![]() 为坐标原点,且
为坐标原点,且![]() ,求
,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在合作学习小组的一次活动中,甲、乙、丙、丁、戊五位同学被随机地分配承担![]() ,
,![]() ,
,![]() ,
,![]() 四项不同的任务,每个同学只能承担一项任务.
四项不同的任务,每个同学只能承担一项任务.
(1)若每项任务至少安排一位同学承担,求甲、乙两人不同时承担同一项任务的概率;
(2)设这五位同学中承担任务![]() 的人数为随机变量
的人数为随机变量![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com