
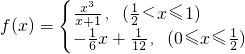 和函数
和函数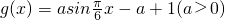 ,若存在x1,x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是
,若存在x1,x2∈[0,1],使得f(x1)=g(x2)成立,则实数a的取值范围是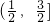

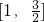
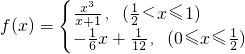 ,
, <x≤1时,f(x)=
<x≤1时,f(x)= ,f′(x)=
,f′(x)=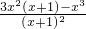 =
=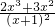 >0,
>0, )<f(x)≤f(1),
)<f(x)≤f(1), ,
, ];
]; 时,f(x)=-
时,f(x)=- x+
x+ ,为减函数,
,为减函数, )≤f(x)≤f(0),
)≤f(x)≤f(0), ],
], ];
];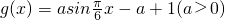 ,g′(x)=
,g′(x)=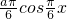 ,0≤
,0≤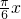 ≤
≤ ,
, ],
],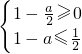 解得
解得 ≤a≤2,
≤a≤2,

 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:高中数学 来源: 题型:
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 4 |
| 3 |
| 3 |
| 2 |
|
查看答案和解析>>
科目:高中数学 来源:2007年南通市教研室高三数学考前预测题 题型:044
已知:函数![]() .
.
(I)证明:f(x)与f-1(x)的交点必在在直线y=x上.
(II)是否存在一对反函数图象的交点不一定在直线y=x上,若存在,请举例说明;若不存,请说明理由.
(III)研究(I)和(II),能否得出一般性的结论,并进行证明.
查看答案和解析>>
科目:高中数学 来源:天津市十二区县重点学校2012届高三毕业班联考(二)数学文科试题 题型:044
已知函数![]() ,其中a为实数.
,其中a为实数.
(Ⅰ)当![]() 时,求函数f(x)的极大值点和极小值点;
时,求函数f(x)的极大值点和极小值点;
(Ⅱ)若对任意a∈(2,3)及x∈[1,3]时,恒有ta2-f(x)>![]() 成立,求实数t的取值范围.
成立,求实数t的取值范围.
(Ⅲ)已知g(x)=a2x2+ax+1,m(x)=![]() x3-(a2+
x3-(a2+![]() )x2+(2a+5)x-3,h(x)=f(x)+m(x),设函数
)x2+(2a+5)x-3,h(x)=f(x)+m(x),设函数![]() 是否存在a,对任意给定的非零实数x1,存在惟一的非零实数x2(x2≠x1),使得
是否存在a,对任意给定的非零实数x1,存在惟一的非零实数x2(x2≠x1),使得![]() (x2)=
(x2)=![]() (x1)成立?若存在,求a的值;若不存,请说明理由.
(x1)成立?若存在,求a的值;若不存,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知:函数![]() (
(![]() ),
),![]() .
.
(1)若函数![]() 图象上的点到直线
图象上的点到直线![]() 距离的最小值为
距离的最小值为![]() ,求
,求![]() 的值;
的值;
(2)关于![]() 的不等式
的不等式![]() 的解集中的整数恰有3个,求实数
的解集中的整数恰有3个,求实数![]() 的取值范围;
的取值范围;
(3)对于函数![]() 与
与![]() 定义域上的任意实数
定义域上的任意实数![]() ,若存在常数
,若存在常数![]() ,使得不等式
,使得不等式![]() 和
和
![]() 都成立,则称直线
都成立,则称直线![]() 为函数
为函数![]() 与
与![]() 的“分界线”。设
的“分界线”。设![]() ,
,
![]() ,试探究
,试探究![]() 与
与![]() 是否存在“分界线”?若存在,求出“分界线”的方程;若不存
是否存在“分界线”?若存在,求出“分界线”的方程;若不存
在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com