
 ,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.(12分)
,且各次投篮的结果互不影响.甲同学决定投5次,乙同学决定投中1次就停止,否则就继续投下去,但投篮次数不超过5次.(12分) 的分布列和数学期望.
的分布列和数学期望. 核心素养学练评系列答案
核心素养学练评系列答案 单元期中期末卷系列答案
单元期中期末卷系列答案科目:高中数学 来源:不详 题型:解答题
 ,否则其获胜的概率为
,否则其获胜的概率为 .
. 为比赛结束时甲的得分,求随机变量
为比赛结束时甲的得分,求随机变量 的分布列及数学期望
的分布列及数学期望 .
.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 ,且相互间没有影响.
,且相互间没有影响. ,试求
,试求 的分布列和数学期望.
的分布列和数学期望.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 8 |
| 15 |
| 1 |
| 15 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 车辆数 | 5 | 10 | 30 | 35 | 15 | 3 | 2 |
| 出租天数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 车辆数 | 14 | 20 | 20 | 16 | 15 | 10 | 5 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ,得2分的概率为
,得2分的概率为 ,不得分的概率为
,不得分的概率为 (
( 、
、 、
、 ),已知他投篮一次得分的数学期望为2(不计其它得分情况),则
),已知他投篮一次得分的数学期望为2(不计其它得分情况),则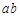 的最大值为( )
的最大值为( )A. | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com