练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    现时盛行的足球彩票，其规则如下：全部13场足球比赛，每场比赛有3种结果：胜、平、负，13长比赛全部猜中的为特等奖，仅猜中12场为一等奖，其它不设奖，则某人获得特等奖的概率为        。


    由题设，此人猜中某一场的概率为，且猜中每场比赛结果的事件为相互独立事件，故某人全部猜中即获得特等奖的概率为。
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

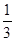    “蛟龙号”从海底中带回的某种生物，甲乙两个生物小组分别独立开展对该生物离开恒温箱的成活情况进行研究，每次试验一个生物，甲组能使生物成活的概率为，乙组能使生物成活的概率为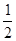，假定试验后生物成活，则称该试验成功，如果生物不成活，则称该次试验是失败的．
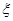    （1）甲小组做了三次试验，求至少两次试验成功的概率；
    （2）如果乙小组成功了4次才停止试验，求乙小组第四次成功前共有三次失败，且恰有两次连续失败的概率；
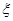    （3）若甲乙两小组各进行2次试验，设试验成功的总次数为，求的期望．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

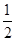    设A、B、C三个事件相互独立，事件A发生的概率是，A、B、C中只有一个发生的概率为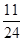，A、B、C中只有一个不发生的概率是。
    （1）求事件B发生的概率及事件C发生的概率；
    （2）试求A、B、C均不发生的概率。

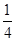    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

     某售货员负责在甲、乙、丙三个柜面上售货．如果在某一小时内各柜面不需要售货员照顾的概率分别为0.9,0.8，0.7．假定各个柜面是否需要照顾相互之间没有影响，求在这个小时内：
    （1）只有丙柜面需要售货员照顾的概率；
    （2）三个柜面最多有一个需要售货员照顾的概率；
    （3）三个柜面至少有一个需要售货员照顾的概率．

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题


    甲：105   102  97  96  100       乙：100  101  102  97  100
    （I）分别求甲、乙的样本平均数与方差，并由此估计谁加工的零件较好？
    （II）若从乙样本的5件产品中再次随机抽取2件，试求这2件产品中至少有一件产品直径为100mm的概率

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    甲、乙两人破译一种密码，它们能破译的概率分别为和，求：
    （1）恰有一人能破译的概率；（2）至多有一人破译的概率；
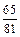    （3）若要破译出的概率为不小于，至少需要多少甲这样的人？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

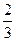    某部队进行射击训练，每个学员最多只能射击4次，学员如有2次命中目标，那么就不再继续射击。假设某学员每次命中目标的概率都是，每次射击互相独立。
    （1）求该学员在前两次射击中至少有一次命中目标的概率；
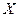    （2）记该学员射击的次数为，求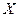的分布列及数学期望。

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    若事件与相互独立，且，则的值等于        .

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    19．（本小题满分12分）
    有甲、乙两箱产品，甲箱共装8件，其中一等品5件，二等品3件；乙箱共装4件，其中一等品3件，二等品1件．现采用分层抽样方法（层内采用不放回简单随机抽样）从甲、乙两箱中共抽取产品3件．
    （Ⅰ）求从甲、乙两箱中各抽取产品的件数；
    （Ⅱ）求抽取的3件产品中至少有2件是一等品的概率．

    查看答案和解析>>

    同步练习册答案