
| A. | $\frac{1}{24}$ | B. | $\frac{1}{12}$ | C. | $\frac{1}{6}$ | D. | $\frac{1}{2}$ |
分析 分别考虑第一个字母刚好为r,第二个字母刚好为o,第三个字母刚好为o的可能性,即可求得结论.
解答 解:第一个字母刚好为r的可能性为$\frac{1}{4}$,
第二个字母刚好为o的可能性为$\frac{2}{3}$(在剩下的o,o,t三个字母中选),
第三个字母刚好为o的可能性为$\frac{1}{2}$(在剩下的o,t两个字母中选)
故将这四个字母随机地排成一行,恰好排成英文单词“root”的概率为 $\frac{1}{4}$×$\frac{2}{3}$×$\frac{1}{2}$=$\frac{1}{12}$,
故选:B
点评 本题考查等可能事件的概率,解题的关键是确定字母在各个位置的可能性,属于中档题.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:高中数学 来源: 题型:选择题
| A. | y=3-x | B. | y=x2-3x | C. | $f(x)={(\frac{1}{2})^x}$ | D. | f(x)=|x| |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$$\overrightarrow{a}$-$\frac{4}{5}$$\overrightarrow{b}$ | B. | $\frac{2}{5}$$\overrightarrow{a}$+$\frac{4}{5}$$\overrightarrow{b}$ | C. | -$\frac{2}{5}$$\overrightarrow{a}$+$\frac{4}{5}$$\overrightarrow{b}$ | D. | -$\frac{2}{5}$$\overrightarrow{a}$-$\frac{4}{5}$$\overrightarrow{b}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 优秀 | 非优秀 | 总计 | |
| 参加数学第二课堂活动 | p | ||
| 未参加数学第二课堂活动 | q | 100 | |
| 总计 | 200 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
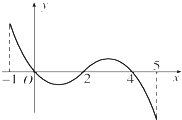 已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.
已知函数f(x)的定义域为[-1,5],f(x)的导函数f′(x)的图象如图所示.若f(x)在区间[m,m+1]上是单调函数,则实数m的取值范围是{m|m=-1或0≤m≤1或2≤m≤3或m=4}.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (x-2)2+(y-1)2=$\sqrt{5}$ | B. | (x-2)2+(y-1)2=5 | C. | (x+2)2+(y+1)2=$\sqrt{5}$ | D. | (x+2)2+(y+1)2=5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | p∨(¬q) | B. | p∧(¬q) | C. | p∨q | D. | p∧q |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com