
分析 利用S△DBM:S${\;}_{△{O}_{1}{B}_{1}M}$=2:3,求出BM,再求出${S}_{△{O}_{1}DM}$,即可求出四面体O1ADM的体积.
解答 解:设BM=x,BD=$\sqrt{2}$,O1B=$\frac{\sqrt{2}}{2}$,
∵S△DBM:S${\;}_{△{O}_{1}{B}_{1}M}$=2:3,
∴$\frac{1}{2}•\sqrt{2}•x$:$\frac{1}{2}•\frac{\sqrt{2}}{2}•(1-x)$=2:3,
∴x=$\frac{1}{4}$,
∴${S}_{△{O}_{1}DM}$=$\frac{1}{2}×\sqrt{2}×1$-$\frac{1}{2}×\frac{\sqrt{2}}{2}×\frac{3}{4}$-$\frac{1}{2}×\sqrt{2}×\frac{1}{4}$=$\frac{3}{16}\sqrt{2}$
∴四面体O1ADM的体积为${V}_{A-{O}_{1}DM}$=$\frac{1}{3}×\frac{3}{16}\sqrt{2}×\frac{\sqrt{2}}{2}$=$\frac{1}{16}$.
故答案为:$\frac{1}{16}$.
点评 本题考查求四面体O1ADM的体积,考查三角形面积的计算,考查学生的计算能力,属于中档题.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{9}{2}$ | B. | $\frac{7}{2}$ | C. | 2$\sqrt{2}$+$\frac{1}{2}$ | D. | 2$\sqrt{2}$-$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
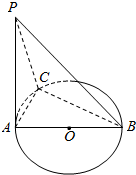 AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点.
AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上不同于A,B的任意一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
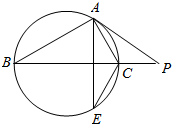 若图中,PA切⊙O于点A,PCB交⊙O于C、B两点,且PCB过点O,AE⊥BP交⊙O于E,则图中与∠CAP相等的角的个数是( )
若图中,PA切⊙O于点A,PCB交⊙O于C、B两点,且PCB过点O,AE⊥BP交⊙O于E,则图中与∠CAP相等的角的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
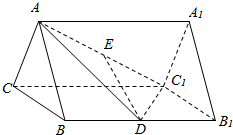 在三棱柱ABC-A1B1C1中,△ABC是边长为2正三角形,D、E分别是线段BB1、AC1的中点,DE⊥AC1.
在三棱柱ABC-A1B1C1中,△ABC是边长为2正三角形,D、E分别是线段BB1、AC1的中点,DE⊥AC1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com