
分析:
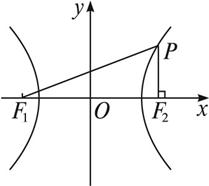
由于PF2⊥x轴,因而可求得P点的纵坐标,即可知|PF2|的值,结合△PF1F2为直角三角形及双曲线的定义,可求得a、b间的关系,就可求得渐近线的斜率.
解法一:
设F2(c,0)(c>0),P(c,y0),
则![]()
∴|PF2|=![]() .
.
在Rt△PF2F1中,∠PF1F2=30°,|F1F2|=![]() |PF2|,即2c=
|PF2|,即2c=![]() ·
·![]() ,将c2=a2+b2代入,
,将c2=a2+b2代入,
解得b2=2a2,故![]()
∴双曲线的渐近线方程为y=±![]() x.
x.
解法二:设F2(c,0)(c>0),P(c,y0),
则![]()
∴|PF2|=![]() .
.
在Rt△PF2F1中,∠PF1F2=30°,|PF1|=2|PF2|,由双曲线的定义可知|PF1|-|PF2|=2a,得|PF2|=2a,
∵|PF2|=![]() ,∴2a=
,∴2a=![]() ,即b2=2a2.
,即b2=2a2.
∴![]()
∴双曲线的渐近线方程为y=±2x.
绿色通道:
双曲线上一点P与两焦点F1、F2连结形成的△PF1F2,是常遇到的一种图形,它往往把三角形的相关知识(如勾股定理、正弦定理、余弦定理、三角形面积公式等)与双曲线的相关知识相结合构造不同的问题,总结对应的解题思路与方法,可从以上的知识入手.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
 如图,已知F1、F2是椭圆C:
如图,已知F1、F2是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| PF1 |
| PF2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知F1,F2是椭圆C:
如图,已知F1,F2是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•鹰潭一模)如图,已知F1,F2是椭圆C:
(2012•鹰潭一模)如图,已知F1,F2是椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,已知F1、F2分别为椭圆C1:
如图,已知F1、F2分别为椭圆C1:| y2 |
| a2 |
| x2 |
| b2 |
| 5 |
| 3 |
| AP |
| PB |
| AQ |
| QB |
查看答案和解析>>
科目:高中数学 来源: 题型:
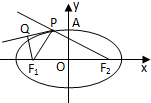 如图,已知F1、F2是椭圆
如图,已知F1、F2是椭圆| x2 |
| 172 |
| y2 |
| 152 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com