
【题目】已知函数![]() (
(![]() ),
),![]() .
.
(1)当![]() 在
在![]() 处的切线与直线
处的切线与直线![]() 垂直时,方程
垂直时,方程![]() 有两相异实数根,求
有两相异实数根,求![]() 的取值范围;
的取值范围;
(2)若幂函数![]() 的图象关于
的图象关于![]() 轴对称,求使不等式
轴对称,求使不等式![]() 在
在![]() 上恒成立的
上恒成立的![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】分析:(1)由题设可得![]() ,令
,令![]() (
(![]() ),利用导数研究函数的单调性,可得
),利用导数研究函数的单调性,可得![]() ,从而可得结果;(2)由题设有
,从而可得结果;(2)由题设有![]() ,令
,令![]() (
(![]() ),两次求导,分两种情况讨论,可得①
),两次求导,分两种情况讨论,可得①![]() 时
时![]() ;②
;②![]() 时,
时,![]() ,综合两种情况可得结果.
,综合两种情况可得结果.
详解:(1)由题设可得![]() ,令
,令![]() (
(![]() )
)
则![]() 令
令![]() 得
得![]() .
.
|
|
|
|
|
|
|
|
| 递减 | 极小值 | 递增 |
∵![]() ,
,![]() ,
,![]() ,
,![]()
且![]() 有两个不等实根,∴
有两个不等实根,∴![]() ,
,
即![]()
∴![]()
(2)由题设有![]() ,令
,令![]() (
(![]() ),
),
则![]() ,令
,令![]() ,则
,则
![]() 又
又![]() ,∴
,∴![]() .∴
.∴![]() 在
在![]() 在单调递增.
在单调递增.
又![]() ,
,
①![]() ,即
,即![]() 时,
时,![]() .
.
所以![]() 在
在![]() 内单调递增,
内单调递增,![]() ,所以
,所以![]()
②![]() ,即
,即![]() 时,由
时,由![]() 在
在![]() 内单调递增,
内单调递增,
且∵![]() ,
,![]() .
.
∴![]() 使得
使得![]() .
.
|
|
|
|
|
|
|
|
| 递减 | 极小值 | 递增 |
所以![]() 的最小值为
的最小值为![]() .
.
又![]() ,所以
,所以![]()
![]() .
.
因此,要使当![]() 时,
时,![]() 恒成立,只需
恒成立,只需![]() ,即
,即![]() 即可.
即可.
解得![]() ,此时
,此时![]() ,可得
,可得![]() ,
,
以下求出![]() 的取值范围.
的取值范围.
设![]() ,
,![]() ,得
,得![]() .
.
所以![]() 在
在![]() 上单调递减,从而
上单调递减,从而![]() .
.
综上①②所述,![]() 的取值范围
的取值范围![]() .
.


科目:高中数学 来源: 题型:
【题目】某学校研究性学习小组调查学生使用智能手机对学习成绩的影响,询问了 30 名同学,得到如下的 ![]() 列联表:
列联表:
使用智能手机 | 不使用智能手机 | 总计 | |
学习成绩优秀 | 4 | 8 | 12 |
学习成绩不优秀 | 16 | 2 | 18 |
总计 | 20 | 10 | 30 |
(Ⅰ)根据以上![]() 列联表判断,能否在犯错误的概率不超过 0.005 的前提下认为使用智能手机对学习成绩有影响?
列联表判断,能否在犯错误的概率不超过 0.005 的前提下认为使用智能手机对学习成绩有影响?
(Ⅱ)从使用学习成绩优秀的 12 名同学中,随机抽取 2 名同学,求抽到不使用智能手机的人数![]() 的分布列及数学期望.智能手机的 20 名同学中,按分层抽样的方法选出 5 名同学,求所抽取的 5 名同学中“学习成绩优秀”和“学习成绩不优秀”的人数;
的分布列及数学期望.智能手机的 20 名同学中,按分层抽样的方法选出 5 名同学,求所抽取的 5 名同学中“学习成绩优秀”和“学习成绩不优秀”的人数;
(Ⅲ)从问题(Ⅱ)中倍抽取的 5 名同学,再随机抽取 3 名同学,试求抽取 3 名同学中恰有 2 名同学为“学习成绩不优秀”的概率.
参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.05 | 0,。025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是某班级50名学生订阅数学、语文、英语学习资料的情况,其中A表示订阅数学学习资料的学生,B表示订阅语文学习资料的学生,C表示订阅英语学习资料的学生

(1)从这个班任意选择一名学生,用自然语言描述1,4,5,8各区域所代表的事件;
(2)用A,B,C表示下列事件:
①恰好订阅一种学习资料;
②没有订阅任何学习资料.
查看答案和解析>>
科目:高中数学 来源: 题型:
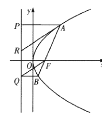
【题目】如图,抛物线![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上
上![]() 两点,在抛物线的准线上的射影分别为
两点,在抛物线的准线上的射影分别为![]() .
.
(1)如图,若![]() 点在线段
点在线段![]() 上,过
上,过![]() 作
作![]() 的平行线
的平行线![]() 与抛物线准线交于
与抛物线准线交于![]() ,证明:
,证明:![]() 是
是![]() 的中点;
的中点;
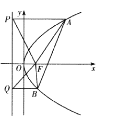
(2)如图,若![]() 的面积是
的面积是![]() 的面积的两倍,求
的面积的两倍,求![]() 中点的轨迹方程.
中点的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知二次函数f(x)满足条件f(0)=1,及f(x+1)﹣f(x)=2x.
(1)求函数f(x)的解析式;
(2)在区间[﹣1,1]上,y=f(x)的图象恒在y=2x+m的图象上方,试确定实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点F为抛物线C:x2=2py (p>0) 的焦点,点A(m,3)在抛物线C上,且|AF|=5,若点P是抛物线C上的一个动点,设点P到直线![]() 的距离为
的距离为![]() ,设点P到直线
,设点P到直线![]() 的距离为
的距离为![]() .
.
(1)求抛物线C的方程;
(2) 求![]() 的最小值;
的最小值;
(3)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=loga(x+1)-loga(1-x),a>0且a≠1.
(1)求f(x)的定义域;
(2)判断f(x)的奇偶性并予以证明;
(3)当a>1时,求使f(x)>0的解集.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解甲、乙两种离子在小鼠体内的残留程度,进行如下试验:将200只小鼠随机分成![]() 两组,每组100只,其中
两组,每组100只,其中![]() 组小鼠给服甲离子溶液,
组小鼠给服甲离子溶液,![]() 组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:
组小鼠给服乙离子溶液.每只小鼠给服的溶液体积相同、摩尔浓度相同.经过一段时间后用某种科学方法测算出残留在小鼠体内离子的百分比.根据试验数据分别得到如下直方图:

记![]() 为事件:“乙离子残留在体内的百分比不低于
为事件:“乙离子残留在体内的百分比不低于![]() ”,根据直方图得到
”,根据直方图得到![]() 的估计值为
的估计值为![]() .
.
(1)求乙离子残留百分比直方图中![]() 的值;
的值;
(2)分别估计甲、乙离子残留百分比的平均值(同一组中的数据用该组区间的中点值为代表).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com