
 某园林公司准备绿化一块半径为200米,圆心角为$\frac{π}{4}$的扇形空地(如图的扇形OPQ区域),扇形的内接矩形ABCD为一水池,其余的地方种花,若∠COP=α,矩形ABCD的面积为S(单位:平方米).
某园林公司准备绿化一块半径为200米,圆心角为$\frac{π}{4}$的扇形空地(如图的扇形OPQ区域),扇形的内接矩形ABCD为一水池,其余的地方种花,若∠COP=α,矩形ABCD的面积为S(单位:平方米).分析 (1)在Rt△OBC中,OB=200cosα,BC=200sinα$(0<α<\frac{π}{4})$,求出BC=200sinα,AB=200cosα-200sinα,得到S=$20000\sqrt{2}sin(2α+\frac{π}{4})-20000$,$(0<α<\frac{π}{4})$即可.
(2)利用三角函数的最值,求解$α=\frac{π}{8}$时,水池的面积S最大,最大面积为$20000\sqrt{2}-20000$平方米.
解答 解:(1)在Rt△OBC中,OB=200cosα,BC=200sinα$(0<α<\frac{π}{4})$…(1分)
在Rt△OAD中,$\frac{DA}{OA}=\;tan\frac{π}{4}=1$,
∴OA=DA=BC=200sinα…(2分)
∴AB=OB-OA=200cosα-200sinα,…(4分)
故S=AB•BC=(200cosα-200sinα)•200sinα
=40000sinαcosα-40000sin2α=20000sin2α-20000(1-cos2α)
=20000(sin2α+cos2α)-20000…(6分)
=$20000\sqrt{2}sin(2α+\frac{π}{4})-20000$,$(0<α<\frac{π}{4})$…(8分)
(2)由$0<α<\frac{π}{4}$,得$\frac{π}{4}<2α+\frac{π}{4}<\frac{3π}{4}$,
所以当$2α+\frac{π}{4}=\frac{π}{2}$,即$α=\frac{π}{8}$时,…(9分)
S最大=$20000\sqrt{2}-20000$…(11分)
因此,当$α=\frac{π}{8}$时,水池的面积S最大,最大面积为$20000\sqrt{2}-20000$平方米 …(12分)
点评 本题考查函数的函数的实际应用,三角函数的最值的求法,考查转化思想以及计算能力.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 22016-2 | B. | 22017-1 | C. | 22016-1 | D. | 22017-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,1] | B. | [1,2] | C. | [-1,2) | D. | (-1,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
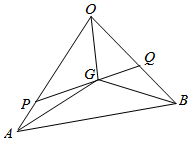 已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,点G是△OAB的重心,过点G的直线PQ与OA、OB分别交于P、Q两点.
已知$\overrightarrow{OA}$=$\overrightarrow{a}$,$\overrightarrow{OB}$=$\overrightarrow{b}$,点G是△OAB的重心,过点G的直线PQ与OA、OB分别交于P、Q两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com