
分析 利用向量垂直的性质推导出b2+c2-a2=-bc,由此利用余弦定理能求出角A的大小.
解答 解:∵在△ABC中,a,b,c分别为角A,B,C所对的边,
向量$\vec m$=(b,c-a),$\vec n$=(b-c,c+a),$\vec m⊥\vec n$,
∴$\overrightarrow{m}•\overrightarrow{n}$=b(b-c)+(c-a)(c+a)=b2+bc+c2-a2=0,
∴b2+c2-a2=-bc,
cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{-bc}{2bc}$=-$\frac{1}{2}$,
∴A=$\frac{2π}{3}$.
故答案为:$\frac{2π}{3}$.
点评 本题考查角的求法,是基础题,解题时要认真审题,注意向量垂直、余弦定理的合理运用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
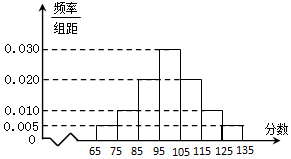 某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:
某校高二年级在一次数学测验后,随机抽取了部分学生的数学成绩组成一个样本,得到如下频率分布直方图:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,m∥β,则α∥β | B. | 若m⊥α,α⊥β,则 m∥β | ||
| C. | 若m?α,m⊥β,则 α⊥β | D. | 若m?α,α⊥β,则 m⊥β |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | c<b<a | B. | c<a<b | C. | a<b<c | D. | a<c<b |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {3} | B. | {2,3} | C. | {1,2,3} | D. | {0,1,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 某园林公司准备绿化一块半径为200米,圆心角为$\frac{π}{4}$的扇形空地(如图的扇形OPQ区域),扇形的内接矩形ABCD为一水池,其余的地方种花,若∠COP=α,矩形ABCD的面积为S(单位:平方米).
某园林公司准备绿化一块半径为200米,圆心角为$\frac{π}{4}$的扇形空地(如图的扇形OPQ区域),扇形的内接矩形ABCD为一水池,其余的地方种花,若∠COP=α,矩形ABCD的面积为S(单位:平方米).查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com