
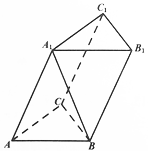
 在三棱柱ABC-A1B1C1中,△ABC是正三角形,且A1A=AB,顶点A1在底面ABC上的射影是△ABC的中心.
在三棱柱ABC-A1B1C1中,△ABC是正三角形,且A1A=AB,顶点A1在底面ABC上的射影是△ABC的中心.分析 (1)由A1O⊥底面ABC,得A1O⊥BC,再由O是△ABC的中心,连接AO交BC于D,则AD⊥BC,由线面垂直的判定可得BC⊥平面A1AD,进一步得到AA1⊥BC;
(2)取B1C1的中点D1,连接A1D1,DD1,由(1)知,BC⊥平面ADD1A1,由线面垂直的判定和性质可得直线A1B与平面BCC1B1所成角.求解直角三角形得答案.
解答 (1)证明:如图,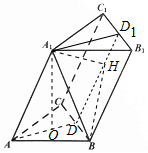
∵A1O⊥底面ABC,∴A1O⊥BC,
∵△ABC为正三角形,O为底面三角形的中心,
连接AO交BC于D,则AD⊥BC,
又AD∩A1D=O,∴BC⊥平面A1AD,
则AA1⊥BC;
(2)解:取B1C1的中点D1,连接A1D1,DD1,
由(1)知,BC⊥平面ADD1A1,
∴平面ADD1A1⊥平面BB1C1C,且平面ADD1A1∩平面BB1C1C=DD1,
过A1作A1H⊥DD1,垂足为H,连接BH,
则∠A1BH为直线A1B与平面BCC1B1所成角.
设A1A=AB=2a,可得${A}_{1}O=\frac{2\sqrt{6}}{3}a$,
由AD•A1O=AA1•A1H,得${A}_{1}H=\frac{AD•{A}_{1}O}{{A}_{1}A}=\frac{\sqrt{3}a•\frac{2\sqrt{6}}{3}a}{2a}$=$\sqrt{2}a$.
在Rt△A1HB中,sin$∠{A}_{1}BH=\frac{\sqrt{2}a}{2a}=\frac{\sqrt{2}}{2}$.
∴直线A1B与平面BCC1B1所成角为45°.
点评 本题考查线面垂直的判定和性质,考查了线面角的求法,考查空间想象能力和思维能力,是中档题.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{5}{4}$ | B. | $\frac{5}{3}$ | C. | $\frac{{\sqrt{7}}}{4}$ | D. | $\frac{25}{16}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=$\frac{1}{x}$ | B. | y=2|x| | C. | y=ln$\frac{1}{|x|}$ | D. | y=x2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若m∥α,m∥β,则α∥β | B. | 若m⊥α,m∥β,则α∥β | C. | 若m⊥α,n∥α,则m∥n | D. | 若m⊥α,n⊥α,则m∥n |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{3}-1}}{2}$ | B. | $\frac{{\sqrt{5}-1}}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,1] | B. | [0,2] | C. | [1,2] | D. | [1,3] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com