

解析:用相关的函数知识,进行合理设计,确定最佳解题关系,进行数学上的计算求解,学会分析、处理数据,初步运用函数思想理解和处理现实生活和社会中的简单问题.
答案:考查近几十年的资料:
年 份 | 人口数 | 10年中增长的倍数 |
1920 | 106 020 000 |
|
1930 | 123 200 000 | 1.162 |
1940 | 132 160 000 | 1.073 |
1950 | 151 330 000 | 1.145 |
1960 | 179 320 000 | 1.185 |
1970 | 203 300 000 | 1.134 |
1980 | 226 540 000 | 1.114 |
从1920年到1930年中,平均每年增长![]() ≈1.015;而从1920年到1980年这60年来看,通过类似计算,平均每年增长率约为1.103.以这段时期的中间年份1950年的人口数作为初始数据,记x为年份数,则对该国人口数y(百万)的较好的一个近似的指数函数模型为y=151·(1.013)x-1950.以此为据,可以预测到2000年时,这个国家的人口数为151·(1.013)2000-1950=151·(1.013)50≈288 000 000(人).
≈1.015;而从1920年到1980年这60年来看,通过类似计算,平均每年增长率约为1.103.以这段时期的中间年份1950年的人口数作为初始数据,记x为年份数,则对该国人口数y(百万)的较好的一个近似的指数函数模型为y=151·(1.013)x-1950.以此为据,可以预测到2000年时,这个国家的人口数为151·(1.013)2000-1950=151·(1.013)50≈288 000 000(人).
很自然地,也会提出“什么时候,该国的人口数达到4亿”这样一类的问题,这也就是在现在的指数函数模型中,已知y,求指数x的问题,正是我们所熟悉的对数函数.若对前面所给出的1790—1980年的数据资料作更为详尽的分析,便可以得到在不同时期,该国的人口数y(百万)所满足的指数函数模型
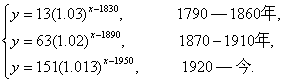


科目:高中数学 来源: 题型:
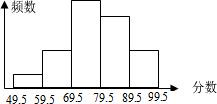
 5、某校组织学生进行了一次社会调查,并对学生的调查报告进行评比.下面是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频数分布直方图.已知从左到右4个组的频率分别是0.05,0.15,0.35,0.30,那么这次评比被评为优秀的调查报告有(分数>或等于80分为优秀,且分数为整数)
5、某校组织学生进行了一次社会调查,并对学生的调查报告进行评比.下面是将某年级60篇学生调查报告的成绩进行整理,分成5组画出的频数分布直方图.已知从左到右4个组的频率分别是0.05,0.15,0.35,0.30,那么这次评比被评为优秀的调查报告有(分数>或等于80分为优秀,且分数为整数)
查看答案和解析>>
科目:高中数学 来源: 题型:
 武汉市某校在“创新素质实践行”活动中组织学生进行社会调查,并对学生的调查报告进行评比,下面是将某年级60篇学生调查报告的成绩进行整理,分成五组画出的频数分布直方图.已知从左至右5个小组的频数之比为1:3:7:6:3,则在这次评比中被评为优秀的调查报告(分数大于或等于80分为优秀,且分数为整数)占百分之( )
武汉市某校在“创新素质实践行”活动中组织学生进行社会调查,并对学生的调查报告进行评比,下面是将某年级60篇学生调查报告的成绩进行整理,分成五组画出的频数分布直方图.已知从左至右5个小组的频数之比为1:3:7:6:3,则在这次评比中被评为优秀的调查报告(分数大于或等于80分为优秀,且分数为整数)占百分之( )| A、45 | B、46 | C、47 | D、48 |
查看答案和解析>>
科目:高中数学 来源: 题型:
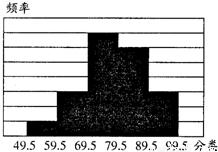
 某校组织学生进行社会调查,并对学生的调查报告进行了评比,分数大于或等于80分为优秀,且分数为整数,下面是将某年级60篇学生调查报告的成绩进行整理,分成5组画出频率分布直方图,已知从左至右4个小组的频率分别是0.05,0.15,0.35,0.30.求在这次评比中被评为优秀的调查报告有多少篇?
某校组织学生进行社会调查,并对学生的调查报告进行了评比,分数大于或等于80分为优秀,且分数为整数,下面是将某年级60篇学生调查报告的成绩进行整理,分成5组画出频率分布直方图,已知从左至右4个小组的频率分别是0.05,0.15,0.35,0.30.求在这次评比中被评为优秀的调查报告有多少篇?查看答案和解析>>
科目:高中数学 来源:2010年江苏省宿迁市高考数学模拟试卷(二)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com