
 )的部分图象.
)的部分图象. =
= ,0<α<
,0<α< ,求cosα的值.
,求cosα的值.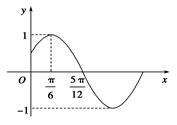
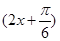 .
. )-
)- ]=cos
]=cos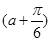 cos
cos +sin
+sin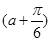 sin
sin =
=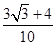 .
.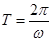 可求ω;由函数的图象过
可求ω;由函数的图象过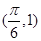 代入可得φ.
代入可得φ.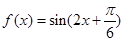 ,从而由
,从而由 ,代入整理可得
,代入整理可得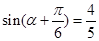
 ,可得利用
,可得利用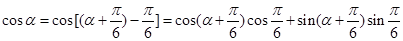 代入求值即可.
代入求值即可.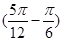 =π,故ω=
=π,故ω=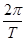 =2.……3分
=2.……3分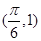 代入f(x)的解析式得sin
代入f(x)的解析式得sin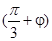 =1,
=1,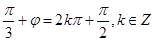 ,即
,即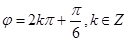 ,
, ,∴φ=
,∴φ= .………………………………5分
.………………………………5分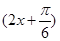 .…………………6分
.…………………6分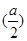 =
= ,得sin
,得sin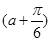 =
= ,由0<α<
,由0<α< ,得
,得 <α+
<α+ <
< ,
,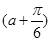 =
=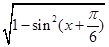 =
=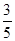 .………………………9分
.………………………9分 )-
)- ]=cos
]=cos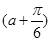 cos
cos +sin
+sin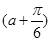 sin
sin =
=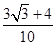 .………12分
.………12分

科目:高中数学 来源:不详 题型:解答题
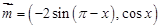 ,
,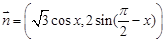 ,函数
,函数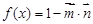 .
.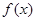 的解析式;
的解析式;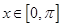 时,求
时,求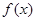 的单调递增区间;
的单调递增区间;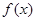 的图象可以由
的图象可以由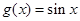 的图象经过怎样的变换而得到.
的图象经过怎样的变换而得到. 查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
 ②
② ;
; ; ④
; ④ 其中“互为生成”函数的是( )
其中“互为生成”函数的是( )| A.①② | B.②③ | C.③④ | D.①④ |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
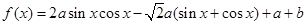 的定义域为
的定义域为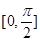 ,值域为
,值域为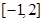 .
.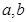 的值;
的值;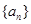 中,有
中,有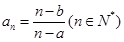 . 则该数列有最大项、最小项吗?若有,求出数列的最大项、最小项;若没有,请说明理由.
. 则该数列有最大项、最小项吗?若有,求出数列的最大项、最小项;若没有,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com