
分析 ①画可行域②明确目标函数几何意义,目标函数表示动点P(x,y)与定点O(0,0)连线斜率k再加1,③过O做直线与可行域相交可计算出直线PO斜率,从而得出所求目标函数范围.
解答 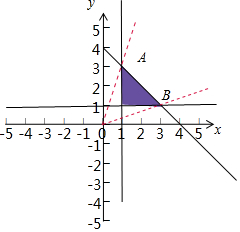 解:先画出可行域如图:
解:先画出可行域如图:
因为目标函数表示动点P(x,y)与定点O(0,0)连线斜率k再加1;
由图可知;
KOB最小,KOA最大;
联立$\left\{\begin{array}{l}{x=1}\\{x+y=4}\end{array}\right.$可得A(1,3)
联立$\left\{\begin{array}{l}{y=1}\\{x+y=4}\end{array}\right.$可得B(3,1).
故:KOB=$\frac{1-0}{3-0}$=$\frac{1}{3}$,KOA=$\frac{3-0}{1-0}$=3,
∴$\frac{1}{3}$≤KOP≤3,
所以:$\frac{x+y}{x}$=1+k∈[$\frac{4}{3}$,4].
故答案为:[$\frac{4}{3}$,4].
点评 本题考查线性规划问题,难点在于目标函数几何意义,近年来高考线性规划问题高考数学考试的热点,数形结合是数学思想的重要手段之一,是连接代数和几何的重要方法.随着要求数学知识从书本到实际生活的呼声不断升高,线性规划这一类新型数学应用问题要引起重视.


科目:高中数学 来源: 题型:解答题
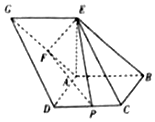 如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE
如图,已知四边形ABCD和ABEG均为平行四边形,点E在平面ABCD内的射影恰好为点A,以BD为直径的圆经过点A,C,AG的中点为F,CD的中点为P,且AD=AB=AE查看答案和解析>>
科目:高中数学 来源: 题型:选择题
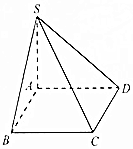 如图,已知四棱锥S-ABCD的底面为矩形且SA⊥底面ABCD,若侧棱SC=5$\sqrt{2}$,则此四棱锥的外接球表面积为( )
如图,已知四棱锥S-ABCD的底面为矩形且SA⊥底面ABCD,若侧棱SC=5$\sqrt{2}$,则此四棱锥的外接球表面积为( )| A. | 25π | B. | 50π | C. | 100π | D. | 200π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{1}{2}$,2) | B. | ($\frac{1}{2}$,+∞) | C. | (0,+∞) | D. | (0,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
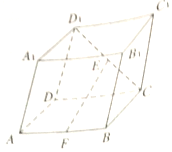 如图,四棱柱ABCD-A1B1C1D1的底面ABCD为矩形,平面CDD1C1⊥平面ABCD,E,F分别是CD,AB的中点,求证:
如图,四棱柱ABCD-A1B1C1D1的底面ABCD为矩形,平面CDD1C1⊥平面ABCD,E,F分别是CD,AB的中点,求证:查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}+1$ | B. | $\sqrt{5}$ | C. | $\frac{{\sqrt{5}+1}}{2}$ | D. | $\frac{{\sqrt{5}}}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com