
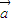 •
•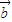 ,其中向量
,其中向量 =(2cosx,1),
=(2cosx,1), =(cosx,
=(cosx, sin2x),x∈R.?
sin2x),x∈R.? ,且x∈[-
,且x∈[-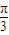 ,
,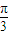 ],求x;?
],求x;?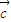 =(m,n),(|m|<
=(m,n),(|m|< )平移后得到函数y=f(x)的图象,求实数m、n的值.
)平移后得到函数y=f(x)的图象,求实数m、n的值.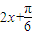 ),通过f(x)=1-
),通过f(x)=1- ,且x∈[-
,且x∈[-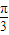 ,
,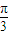 ],得到?sin
],得到?sin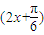 =-
=-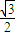 .?求出x的值.
.?求出x的值.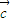 =(m,n),(|m|<
=(m,n),(|m|<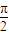 )平移后得到函数y=f(x)的图象,说明两个函数表达式相同,比较两个函数的关系,即可求出实数m、n的值.
)平移后得到函数y=f(x)的图象,说明两个函数表达式相同,比较两个函数的关系,即可求出实数m、n的值.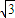 sin2x=1+2sin(
sin2x=1+2sin(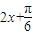 ),
),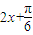 )=1-
)=1-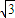 ,
,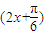 =-
=-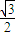 .?
.?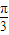 ≤x≤
≤x≤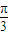 ,
,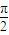 ≤2x+
≤2x+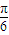 ≤
≤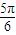 ,?
,?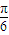 =-
=-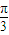 ,即x=-
,即x=-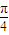 .
.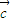 =(m,n)平移后得到函数y=2sin2(x-m)+n的图象,
=(m,n)平移后得到函数y=2sin2(x-m)+n的图象,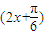 +1,?
+1,?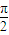 ,
,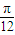 ,n=1.?
,n=1.?

科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| b1 |
| 1 |
| b2 |
| 1 |
| b3 |
| 1 |
| bn |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com