练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知椭圆：的左右焦点分别为，过作垂直于轴的直线交椭圆于两点，且满足.

    （1）求椭圆的离心率；

    （2）过作斜率为的直线交于两点. 为坐标原点，若的面积为，求椭圆的方程.

    【答案】（1）；（2）.

    【解析】

    试题分析：（1）根据题意画出图形可知，则，根据椭圆定义可知：，所以有，所以，整理得：，所以离心率；（2）由（1）得出：，所以椭圆方程为，则左焦点坐标为过的直线方程为：，联立直线方程与椭圆方程，消去未知数，得到关于的一元二次方程，显然，设，于是可以得出和的值（均为含的表达式），将的面积表示成，再转化成，整理后得到关于变量的方程，解出值后，即求出椭圆的标准方程.

    试题解析：（1）点横坐标为，代入椭圆得，

    解得，∴.

    ,∴，∴.

    （2）椭圆方程化为，直线为：，联立可得，…6分

    设，则,得.

    的面积为:

    ，

    ∴,∴椭圆的方程为.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】为增强市民的节能环保意识，郑州市面向全市征召义务宣传志愿者，从符合条件的500名志愿者中随机抽取100名，其年龄频率分布直方图如图所示，其中年龄分组区是：．

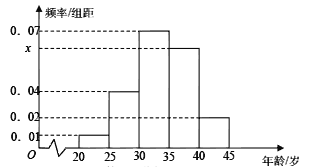
    （Ⅰ）求图中的值，并根据频率分布直方图估计这500名志愿者中年龄在岁的人数；

    （Ⅱ）在抽出的100名志愿者中按年龄采用分层抽样的方法抽取10名参加中心广场的宣传活动，再从这10名志愿者中选取3名担任主要负责人．记这3名志愿者中“年龄低于35岁”的人数为，求的分布列及数学期望．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图1，在边长为1的等边三角形ABC中，D，E分别是AB，AC边上的点，AD=AE，F是BC的中点，AF与DE交于点G，将△ABF沿AF折起，得到如图2所示的三棱锥A﹣BCF，其中BC=．

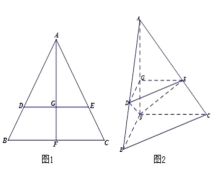
    （Ⅰ）证明：DE∥平面BCF；

    （Ⅱ）证明：CF⊥平面ABF；

    （Ⅲ）当AD=时，求三棱锥F﹣DEG的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知国家某5A级大型景区对拥挤等级与每日游客数量（单位：百人）的关系有如下规定：当时，拥挤等级为“优”；当时，拥挤等级为“良”；当时，拥挤等级为“拥挤”；当时，拥挤等级为“严重拥挤”。该景区对6月份的游客数量作出如图的统计数据：

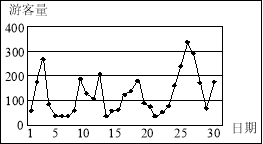
    （Ⅰ）下面是根据统计数据得到的频率分布表，求出的值，并估计该景区6月份游客人数的平均值（同一组中的数据用该组区间的中点值作代表）；

    游客数量

    （单位：百人）

    天数

    频率

    （Ⅱ）某人选择在6月1日至6月5日这5天中任选2天到该景区游玩，求他这2天遇到的游客拥挤等级均为“优”的概率．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    已知过点的直线的参数方程是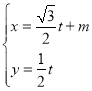（为参数）．以平面直角坐标系的原点为极点，轴的正半轴为极轴，建立极坐标系，曲线的极坐标方程式为.

    （Ⅰ）求直线的普通方程和曲线的直角坐标方程；

    （Ⅱ）若直线与曲线交于两点，且，求实数的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设f(x)＝si n－2cos2＋1.

    (1)求f(x)的最小正周期；

    (2)若函数y＝f(x)与y＝g(x)的图象关于直线x＝1对称，求当x∈时，y＝g(x)的最大值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知中心在坐标原点的椭圆经过点，且点为其右焦点.

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）是否存在平行于的直线，使得直线与椭圆有公共点，且直线与的距离等于4？若存在，求出直线的方程；若不存在，请说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】选修4-4：坐标系与参数方程

    在平面直角坐标系中，曲线的参数方程为（为参数）；在以原点为极点，轴的正半轴为极轴的极坐标系中，曲线的极坐标方程为．

    （I）求曲线的极坐标方程和曲线的直角坐标方程；

    （II）若射线与曲线，的交点分别为（异于原点），当斜率时，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】为了迎接世博会，某旅游区提倡低碳生活，在景区提供自行车出租．该景区有50辆自行车供游客租赁使用，管理这些自行车的费用是每日115元．根据经验，若每辆自行车的日租金不超过6元，则自行车可以全部租出；若超出6元，则每超过1元，租不出的自行车就增加3辆．为了便于结算，每辆自行车的日租金（元）只取整数，并且要求出租自行车一日的总收入必须高于这一日的管理费用，用（元）表示出租自行车的日净收入（即一日中出租自行车的总收入减去管理费用后的所得）。

    （1）求函数的解析式及其定义域；

    （2）试问当每辆自行车的日租金定为多少元时，才能使一日的净收入最多？

    查看答案和解析>>

    同步练习册答案