
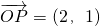 ,
,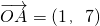 ,
,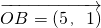 ,设C是直线OP上的一点,其中O为坐标原点.
,设C是直线OP上的一点,其中O为坐标原点. 取得最小值时向量
取得最小值时向量 的坐标;
的坐标; =t
=t =(2t,t).
=(2t,t). =(1,7),
=(1,7), =(2t,t),
=(2t,t), =(5,1),
=(5,1), =
= -
- =(1-2t,7-t),
=(1-2t,7-t), =
= -
- =(5-2t,1-t).
=(5-2t,1-t). •
• =(1-2t)(5-2t)+(7-t)(1+t)=5t2-20t+12=5(t-2)2-8.
=(1-2t)(5-2t)+(7-t)(1+t)=5t2-20t+12=5(t-2)2-8. •
• 取得最小值-8,此时,
取得最小值-8,此时, =(4,2).
=(4,2). =(4,2)时,
=(4,2)时, =(-3,5),
=(-3,5), =(1,-1),
=(1,-1),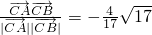 .
. =t
=t =(2t,t),求出
=(2t,t),求出 和
和  的坐标,代入
的坐标,代入 •
• 的式子进行运算,再利用二次函数的性质求出
的式子进行运算,再利用二次函数的性质求出 •
• 的最小值.
的最小值. 和
和 的坐标代入两个向量的夹角公式,求出cos∠ACB 的值.
的坐标代入两个向量的夹角公式,求出cos∠ACB 的值.

 智慧小复习系列答案
智慧小复习系列答案科目:高中数学 来源: 题型:
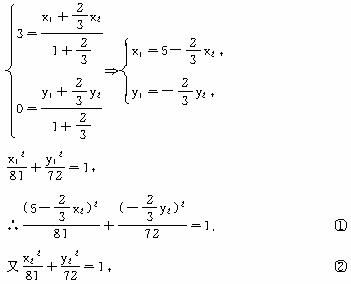
(1)求点P的轨迹方程;
(2)经过点C的直线l与点P的轨迹交于M、N两点,且点C分![]() 所成的比等于2∶3,求直线l的方程.
所成的比等于2∶3,求直线l的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
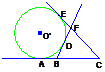
已知A、B、C是直线l上的三点,且|AB|=|BC|=6,⊙O′切直线l于点A,又过B、C作⊙O′异于l的两切线,设这两切线交于点P,求点P的轨迹方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com