
【题目】已知三棱柱ABC﹣A1B1C1的侧棱与底面垂直,体积为 ![]() ,底面是边长为
,底面是边长为 ![]() 的正三角形,若P为底面A1B1C1的中心,则PA与平面A1B1C1所成角的大小为( )
的正三角形,若P为底面A1B1C1的中心,则PA与平面A1B1C1所成角的大小为( )
A.![]()
B.![]()
C.![]()
D.![]()
【答案】B
【解析】解:如图所示,
∵AA1⊥底面A1B1C1 , ∴∠APA1为PA与平面A1B1C1所成角,
∵平面ABC∥平面A1B1C1 , ∴∠APA1为PA与平面ABC所成角.
∵ ![]() =
= ![]() =
= ![]() .
.
∴V三棱柱ABC﹣A1B1C1= ![]() =
= ![]() ,解得
,解得 ![]() .
.
又P为底面正三角形A1B1C1的中心,∴ ![]() =
= ![]() =1,
=1,
在Rt△AA1P中, ![]() ,
,
∴ ![]() .
.
故选B.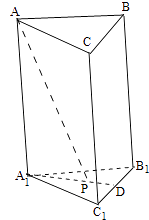
利用三棱柱ABC﹣A1B1C1的侧棱与底面垂直和线面角的定义可知,∠APA1为PA与平面A1B1C1所成角,即为∠APA1为PA与平面ABC所成角.利用三棱锥的体积计算公式可得AA1 , 再利用正三角形的性质可得A1P,在Rt△AA1P中,利用tan∠APA1= ![]() 即可得出.
即可得出.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中数学 来源: 题型:
【题目】如图,在半径为40cm的半圆形(O为圆心)铝皮上截取一块矩形材料ABCD,其中A,B在直径上,点C,D在圆周上、 
(1)设AD=x,将矩形ABCD的面积y表示成x的函数,并写出其定义域;
(2)怎样截取,才能使矩形材料ABCD的面积最大?并求出最大面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知甲、乙两名同学在某项测试中得分成绩的茎叶图如图所示,x1 , x2分别表示知甲、乙两名同学这项测试成绩的众数,s12 , s22分别表示知甲、乙两名同学这项测试成绩的方差,则有( ) 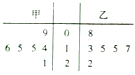
A.x1>x2 , s12<s22
B.x1=x2 , s12>s22
C.x1=x2 , s12=s22
D.x1=x2 , s12<s22
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】分别求出适合下列条件的直线方程: (Ⅰ)经过点P(﹣3,2)且在x轴上的截距等于在y轴上截距的2倍;
(Ⅱ)经过直线2x+7y﹣4=0与7x﹣21y﹣1=0的交点,且和A(﹣3,1),B(5,7)等距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知:θ为第一象限角, ![]() =(sin(θ﹣π),1),
=(sin(θ﹣π),1), ![]() =(sin(
=(sin( ![]() ﹣θ),﹣
﹣θ),﹣ ![]() ),
),
(1)若 ![]() ∥
∥ ![]() ,求
,求 ![]() 的值;
的值;
(2)若| ![]() +
+ ![]() |=1,求sinθ+cosθ的值.
|=1,求sinθ+cosθ的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设直线l的方程为(a+1)x+y+2﹣a=0(a∈R).
(1)若直线l在两坐标轴上的截距相等,求直线l的方程;
(2)若直线l不经过第二象限,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司拟设计一个扇环形状的花坛(如图所示),该扇环是由以点O为圆心的两个同心圆弧和延长后通过点AD的两条线段围成.设圆弧 ![]() 、
、 ![]() 所在圆的半径分别为f(x)、R米,圆心角为θ(弧度).
所在圆的半径分别为f(x)、R米,圆心角为θ(弧度). 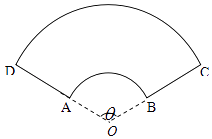
(1)若θ= ![]() ,r1=3,r2=6,求花坛的面积;
,r1=3,r2=6,求花坛的面积;
(2)设计时需要考虑花坛边缘(实线部分)的装饰问题,已知直线部分的装饰费用为60元/米,弧线部分的装饰费用为90元/米,预算费用总计1200元,问线段AD的长度为多少时,花坛的面积最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com