
(本小题满分12分)设{an}是公比为 q?的等比数列,且a1,a3,a2成等差数列.
(1)求q的值;
(2)设{bn}是以2为首项,q为公差的等差数列,其前n项和为Sn,当n≥2时,比较Sn与bn的大小,并说明理由.
(1)q=1或-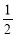 ;(2)当2≤n≤9时,Sn>bn;当n=10时,Sn=bn;当n≥11时,Sn<bn..
;(2)当2≤n≤9时,Sn>bn;当n=10时,Sn=bn;当n≥11时,Sn<bn..
【解析】
试题分析:(1)由题意,根据等比数列和等差中项概念构造方程可得q的值;(2)由(1)得q=1或-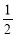 ,故分情况讨论:当q=1时,求得
,故分情况讨论:当q=1时,求得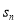 和
和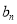 ,然后作差比较大小;当时q=-
,然后作差比较大小;当时q=-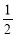 时亦然.
时亦然.
试题解析:(1)由题设2a3=a1+a2,即2a1q2=a1+a1q,
∵a1≠0,∴2q2-q-1=0,∴q=1或-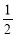 .
.
(2)若q=1,则Sn=2n+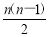 =
=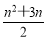 .
.
当n≥2时,Sn-bn=Sn-1=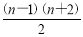 >0,故Sn>bn.
>0,故Sn>bn.
若q=-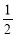 ,则Sn=2n+
,则Sn=2n+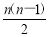 (-
(-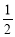 )=
)=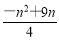 .
.
当n≥2时,Sn-bn=Sn-1=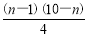 ,
,
故对于n∈N+,当2≤n≤9时,Sn>bn;当n=10时,Sn=bn;当n≥11时,Sn<bn.
考点:等差、等比数列基本概念和求和


科目:高中数学 来源:2015届吉林省长春市高二下学期期中考试理科数学试卷(解析版) 题型:解答题
某工艺厂开发一种新工艺品,头两天试制中,该厂要求每位师傅每天制作10件,该厂质检部每天从每位师傅制作的10件产品中随机抽取4件进行检查,若发现有次品,则当天该师傅的产品不能通过.已知李师傅第一天、第二天制作的工艺品中分别有2件、1件次品.
(1)求两天中李师傅的产品全部通过检查的概率;
(2)若厂内对师傅们制作的工艺品采用记分制,两天都不通过检查的得0分,两天中只通过一天检查的得1分,两天都通过检查的得2分,求李师傅在这两天内得分的数学期望.
查看答案和解析>>
科目:高中数学 来源:2015届吉林省长春市高二下学期期中考试文科数学试卷(解析版) 题型:选择题
设复数 的共轭复数
的共轭复数 满足(1+
满足(1+ )
) =2,其中
=2,其中 为虚数单位,则
为虚数单位,则 等于( )
等于( )
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省高二第一次月考数学试卷(解析版) 题型:选择题
数列 满足
满足 ,且
,且 是递增数列,则实数
是递增数列,则实数 的取值范围是( )
的取值范围是( )
A. B.
B.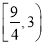 C.(1,3) D.(2,3)
C.(1,3) D.(2,3)
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省沈阳市高二上学期10月月考数学试卷(解析版) 题型:填空题
设平面内有n条直线(n≥3),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用f(n)表示这n条直线交点的个数,当n>4时,f(n)= .
查看答案和解析>>
科目:高中数学 来源:2014-2015学年辽宁省沈阳市高二上学期10月月考数学试卷(解析版) 题型:选择题
已知 ,若z=x+2y的最大值是3,则a的值是( )
,若z=x+2y的最大值是3,则a的值是( )
A.1 B.-1 C. 0 D. 2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com