
(08年龙岩一中模拟)(12分)
如图,三棱锥P―ABC中, PC![]() 平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD
平面ABC,PC=AC=2,AB=BC,D是PB上一点,且CD![]() 平面PAB.
平面PAB.
(Ⅰ) 求证:AB![]() 平面PCB;
平面PCB;
(Ⅱ)求异面直线AP与BC所成角的大小;
(Ⅲ)求二面角C-PA-B的大小的余弦值.

解析:解法一:
(I) ∵PC![]() 平面ABC,
平面ABC,![]()
![]() 平面ABC,∴PC
平面ABC,∴PC![]() AB.
AB.
∵CD![]() 平面PAB,
平面PAB,![]() 平面PAB,∴CD
平面PAB,∴CD![]() AB. …………………………2分
AB. …………………………2分
又![]() ,∴AB
,∴AB![]() 平面PCB. ……………………… 4分
平面PCB. ……………………… 4分
(II) 过点A作AF//BC,且AF=BC,连结PF,CF.
则![]() 为异面直线PA与BC所成的角.………5分
为异面直线PA与BC所成的角.………5分
由(Ⅰ)可得AB⊥BC,∴CF![]() AF.
AF.
由三垂线定理,得PF![]() AF.
AF.
则AF=CF=![]() ,PF=
,PF=![]() ,
,
在![]() 中, tan∠PAF=
中, tan∠PAF=![]() =
=![]() ,
,
∴异面直线PA与BC所成的角为![]() . ……………………………8分
. ……………………………8分
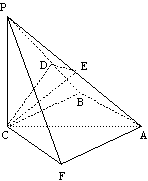
(III)取AP的中点E,连结CE、DE.
∵PC=AC=2, ∴CE ![]() PA,CE=
PA,CE=![]() .
.
∵CD![]() 平面PAB, 由三垂线定理的逆定理,得 DE
平面PAB, 由三垂线定理的逆定理,得 DE![]() PA.
PA.
∴![]() 为二面角C-PA-B的平面角. …………………………………10分
为二面角C-PA-B的平面角. …………………………………10分
由(I) AB![]() 平面PCB,又∵AB=BC,可求得BC=
平面PCB,又∵AB=BC,可求得BC=![]() .
.
在![]() 中,PB=
中,PB=![]() ,
,
![]() .
.
在![]() 中, cos
中, cos![]() =
=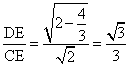 .
.
∴二面角C-PA-B大小的余弦值为![]() . …………………………12分
. …………………………12分
解法二:(I)同解法一. ………4分
(II) 由(I) AB![]() 平面PCB,∵PC=AC=2,又∵AB=BC,可求得BC=
平面PCB,∵PC=AC=2,又∵AB=BC,可求得BC=![]() .
.
以B为原点,如图建立坐标系.
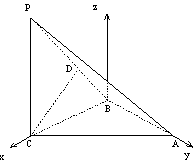
则A(0,![]() ,0),B(0,0,0),
,0),B(0,0,0),
C(![]() ,0,0),P(
,0,0),P(![]() ,0,2).
,0,2).
![]() ,
,![]() .…6分
.…6分
则![]() +0+0=2.
+0+0=2.
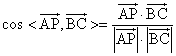 =
=![]() =
= ![]() .
.
∴异面直线AP与BC所成的角为![]() . …………………………8分
. …………………………8分
(III)设平面PAB的法向量为![]() = (x,y,z).
= (x,y,z).
![]() ,
,![]() ,
,
则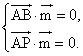 即
即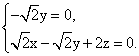
![]()
解得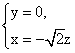 令
令![]() = -1, 得
= -1, 得![]() = (
= (![]() ,0,-1). …………………10分
,0,-1). …………………10分
设平面PAC的法向量为![]() =(
=(![]() ).
).
![]() ,
,![]() ,
,
则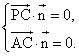 即
即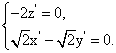
解得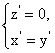 令
令![]() =1, 得
=1, 得 ![]() = (1,1,0).
= (1,1,0).
 =
=![]() .
.
∴二面角C-PA-B大小的余弦值为![]() . ……………………12分
. ……………………12分


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:高中数学 来源: 题型:
(08年龙岩一中模拟文)(12分)
设a、b、c分别是先后三次抛掷一枚骰子得到的点数。
(Ⅰ)求a+b+c为奇数的概率
(Ⅱ)设有关于![]() 的一元二次方程
的一元二次方程![]() ,求上述方程有两个不相等实根的概率.
,求上述方程有两个不相等实根的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年龙岩一中模拟理)(14分)
已知函数![]() ,
,![]() .
.
(1)证明:当![]() 时,
时,![]() 在
在![]() 上是增函数;
上是增函数;
(2)对于给定的闭区间![]() ,试说明存在实数
,试说明存在实数 ![]() ,当
,当![]() 时,
时,![]() 在闭区间
在闭区间![]() 上是减函数;
上是减函数;
(3)证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
(08年龙岩一中模拟)(12分)
盒内有大小相同的9个球,其中2个红色球,3个白色球,4个黑色球. 规定取出1个红色球得1分,取出1个白色球得0分,取出1个黑色球得![]() 分. 现从盒内一次性取3个球.
分. 现从盒内一次性取3个球.
(Ⅰ)求取出的3个球得分之和恰为1分的概率;
(Ⅱ)设![]() 为取出的3个球中白色球的个数,求
为取出的3个球中白色球的个数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com