
����Ŀ��ijҽ�ƿ�����Ŀ��5ֻʵ��С�������ڵ�A��B����ָ�����ݽ����ռ��ͷ������õ����������±���
ָ�� | 1��С���� | 2��С���� | 3��С���� | 4��С���� | 5��С���� |
A | 5 | 7 | 6 | 9 | 8 |
B | 2 | 2 | 3 | 4 | 4 |
��1����ͨ�����ݷ�������֪A��ָ��������B��ָ�����ݾ���������ع�ϵ���Ը����ϱ�����B��ָ������y����A��ָ������x�����Իع鷽�� ![]() =
= ![]() x+
x+ ![]() ��
��
��2����Ҫ����5ֻС�����������ȡ3ֻ��������������һֻB��ָ�����ݸ���3�ĸ��ʣ� �ο���ʽ�� ![]() =
= 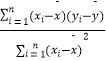 =
=  ��
�� ![]() =
= ![]() ��
�� ![]() ��
��
���𰸡�
��1���⣺�������⣬���� ![]() =
= ![]() ����5+7+6+9+8��=7��
����5+7+6+9+8��=7��
![]() =
= ![]() ����2+2+3+4+4��=3��
����2+2+3+4+4��=3��
![]() =
= 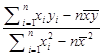 =
= ![]() =
= ![]() =
= ![]() ��
��
![]() =
= ![]() ��
�� ![]() =3��
=3�� ![]() ��7=��
��7=�� ![]() ��
��
��y����x�����Իع鷽��Ϊ ![]() =
= ![]() x��
x�� ![]()
��2���⣺����5ֻС�����������ȡ3ֻ�������¼���Ϊ��
223��224��224��234��234��244��234��234��244��344��10�ֲ�ͬ��ȡ����
����������һֻB��ָ�����ݸ���3�Ļ����¼��ǣ�
224��224��234��234��244��234��234��244��344��9�ֲ�ͬ��ȡ����
������ĸ���ΪP= ![]()
����������1������ ![]() ��
�� ![]() ������ع�ϵ����д���ع鷽�̣���2�������оٷ���������¼�������������ĸ���ֵ��
������ع�ϵ����д���ع鷽�̣���2�������оٷ���������¼�������������ĸ���ֵ��


 ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
ѧ���쳵�����ּ��������ҵ�½����������ϵ�д� �����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д�
�����ѧСѧ�꼶�νӵ������㽭��ѧ������ϵ�д� Сѧ�����ҵ���ϴ�ѧ������ϵ�д�
Сѧ�����ҵ���ϴ�ѧ������ϵ�д� ���Ž�����ٰθ��νӹ㶫���������ϵ�д�
���Ž�����ٰθ��νӹ㶫���������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�������ڽ�A��B��C�ĶԱ߷ֱ���a��b��c���� ����cosBcosC��sinBsinC�����ABCһ���Ƕ۽������Σ�
����acosA=bcosB�����ABC����������
�� ![]() ��
�� ![]() ����
���� ![]() �����ABC���������
�����ABC���������
����OΪ��ABC�����ģ� ![]() ��
��
����sin2A+sin2B=sin2C�� ![]() ��
�� 
����������ȷ������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������S��ABC�У�SA�͵���ABC��AC=AB=SA=2��AC��AB��D��E�ֱ���AC��BC���е㣬F��SE�ϣ���SF=2FE�� 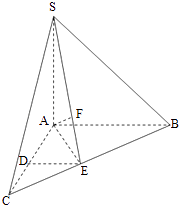
��1����֤��AF��ƽ��SBC��
��2�����߶���DE���Ƿ���ڵ�G��ʹ�����G��AF��E�Ĵ�СΪ30�㣿�����ڣ����DG�ij����������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ѧ����8�㿪ʼ�ϿΣ���ѧ��С����С����������7��40��8��00֮�䵽У���������ڸ�ʱ��ε��κ�ʱ�̵�У���ǵȿ��ܵģ���С���С��������5���ӵ�У�ĸ���Ϊ�� ��
A.![]()
B.![]()
C.![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=ex������eΪ��Ȼ�����ĵ�������g��x��= ![]() x+m��m��n��R����
x+m��m��n��R����
��1����T��x��=f��x��g��x����m=1�� ![]() ����T��x����[0��1]�ϵ����ֵ��
����T��x����[0��1]�ϵ����ֵ��
��2����m=�� ![]() ��n��N* �� ��ʹf��x����ͼ�����g��x��ͼ���Ϸ������������n��[ע�⣺7��e2��
��n��N* �� ��ʹf��x����ͼ�����g��x��ͼ���Ϸ������������n��[ע�⣺7��e2�� ![]() ]��
]��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��mx+ny=1��Բx2+y2=4�Ľ���Ϊ���㣨���������Ϊ�����ĵ㣩��������ֱ�ߵ������ǣ� ��
A.2
B.4
C.6
D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����˶����˶��ֻ����ռ�����ǿ�������˶��Ļ����ԣ�ÿ��һ��Ϊһ�ֽ���ʱ�У�ij��ѧ��ȫУ��Χ���ڻ��������Ͷ���ʦ����չ��ÿ��һ��������������µ���ʵ��ع�����ѧУ���˽�ȫУʦ��ÿ��һ�������ѧУ�綨һ��һ����·����4ǧ��Ϊ���������ʽ��������16ǧ��Ϊ���������ʽ�ߣ�����Ϊһ�����ʽ�ߣ�ѧУί����ѧ����飬��ѧ����÷ֲ�����İ취ȥ����ȫУʦ������������ʵ�ʼ����ڷֲ�������϶�ȫУ��ʦ����Ϊ200�ˣ���һѧ������Ϊ700�ˣ��߶�ѧ������600�ˣ�����ѧ������500�����г�ȡn����Ϊ������õ�����ͼ��ʾ����n�˵�Ƶ�ʷֲ�ֱ��ͼ����n������20�˱�ѧУ�綨Ϊ���������ʽ�ߣ� 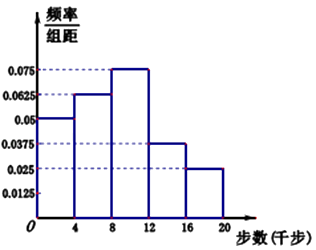
��1���������Ϊ�����������Ľ�ʦ������
��2������Ƶ�ʷֲ�ֱ��ͼ����ȫУʦ��ÿ��һ����·��������λ�����������뾫ȷ������������
��3��У�칫������ȫУʦ�����ټdz�ȡ3����Ϊ��ÿ��һ�����ο�ʶ��ƻ�ѧУ�綨���������ʽ�߱��Ծ������0Ԫ�����������ʽ�߱��ý���20Ԫ��һ�����ʽ�߹����Խ���10Ԫ�����������������壬��Ƶ����Ϊ���ʣ������У�칫��ο�ʽ������X�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������P��ABCD�У�����PA��ƽ��ABCD��EΪAD���е㣬BE��CD��BE��AD��PA=AE=BE=2��CD=1�� 
��1��������C��PB��E������ֵ��
��2�����߶�PE���Ƿ���ڵ�M��ʹ��DM��ƽ��PBC�������ڣ������M��λ�ã��������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=kex��x2������k��R��e����Ȼ�����ĵ�������
������k��0�����жϺ���f��x�������䣨0��+�ޣ��ϵĵ����ԣ�
������k=2����x�ʣ�0��+�ޣ�ʱ���ԱȽ�f��x����2�Ĵ�С��
����������f��x����������ֵ��x1 �� x2��x1��x2������k��ȡֵ��Χ����֤��0��f��x1����1��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com