
 的图象上,且Pn的横坐标构成以-
的图象上,且Pn的横坐标构成以- 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}. +
+ +…+
+…+ 的值.
的值.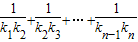
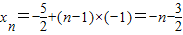 ,
,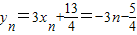 .
.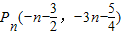 .
.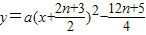 .
.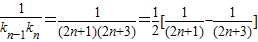 ,
, =
=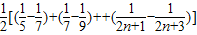
 .
.

科目:高中数学 来源: 题型:
| 13 |
| 4 |
| 5 |
| 2 |
| 1 |
| k1k2 |
| 1 |
| k2k3 |
| 1 |
| knkn+1 |
查看答案和解析>>
科目:高中数学 来源:广西南宁二中2012届高三8月月考数学理科试题 题型:044
在平面直角坐标上有一点列![]() 对一切正整数n,点Pn在函数
对一切正整数n,点Pn在函数![]() 的图象上,且Pn的横坐标构成以
的图象上,且Pn的横坐标构成以![]() 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}.
(Ⅰ)求点Pn的坐标;
(Ⅱ)设抛物线列![]() 中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,n2+1).记与抛物线Cn相切于点Dn的直线的斜率为Kn,求
中的每一条的对称轴都垂直于x轴,抛物线Cn的顶点为Pn,且过点Dn(0,n2+1).记与抛物线Cn相切于点Dn的直线的斜率为Kn,求![]() 的值;
的值;
(Ⅲ)设![]() ,等差数列{an}的任一项an∈S∩T,其中
,等差数列{an}的任一项an∈S∩T,其中![]() 中的最大数,-265<a0<-125,求数列{an}的通项公式.
中的最大数,-265<a0<-125,求数列{an}的通项公式.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 的图象上,且Pn的横坐标构成以-
的图象上,且Pn的横坐标构成以- 为首项,-1为公差的等差数列{xn}.
为首项,-1为公差的等差数列{xn}.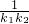 +
+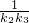 +…+
+…+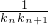 的值.
的值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 13 |
| 4 |
| 5 |
| 2 |
| 1 |
| k1k2 |
| 1 |
| k2k3 |
| 1 |
| knkn+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com