
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| C | 0 3 |
| 2 |
| 3 |
| 1 |
| 27 |
| C | 1 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| C | 2 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
| 9 |
| C | 3 3 |
| 2 |
| 3 |
| 8 |
| 27 |
| 1 |
| 27 |
| 2 |
| 9 |
| 4 |
| 9 |
| 8 |
| 27 |
| C | 2 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 10 |
| 34 |
| C | 3 3 |
| 2 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 2 |
| 4 |
| 35 |
| 10 |
| 34 |
| 4 |
| 35 |
| 34 |
| 243 |


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| 分数(分数段) | 频数(人数) | 频率 |
| [60,70) | 9 | x |
| [70,80) | y | 0.38 |
| [80,90) | 16 | 0.32 |
| [90,100) | z | s |
| 合 计 | p | 1 |
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省高三第一次(3月)周测理科数学试卷(解析版) 题型:解答题
为普及高中生安全逃生知识与安全防护能力,某学校高一年级举办了高中生安全知识与安全逃生能力竞赛. 该竞赛分为预赛和决赛两个阶段,预赛为笔试,决赛为技能比赛.先将所有参赛选手参加笔试的成绩(得分均为整数,满分为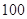 分)进行统计,制成如下频率分布表.
分)进行统计,制成如下频率分布表.
|
分数(分数段) |
频数(人数) |
频率 |
|
[60,70) |
|
|
|
[70,80) |
|
|
|
[80,90) |
|
|
|
[90,100) |
|
|
|
合 计 |
|
|
(Ⅰ)求出上表中的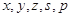 的值;
的值;
(Ⅱ)按规定,预赛成绩不低于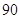 分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一·二班有甲、乙两名同学取得决赛资格.
分的选手参加决赛,参加决赛的选手按照抽签方式决定出场顺序.已知高一·二班有甲、乙两名同学取得决赛资格.
①求决赛出场的顺序中,甲不在第一位、乙不在最后一位的概率;
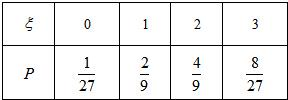
②记高一·二班在决赛中进入前三名的人数为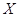 ,求
,求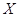 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:2013-2014学年广东省中山二中高三(上)第一次月考数学试卷(理科)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com