
设F1、F2为椭圆![]() 的两个焦点,P为上一点,已知P、F1、F2是一个直角三角形的三个顶点,且|PF1|>|PF2|,求
的两个焦点,P为上一点,已知P、F1、F2是一个直角三角形的三个顶点,且|PF1|>|PF2|,求![]() 的值.
的值.
由已知,|PF1|>|PF2|,|PF1|+|PF2|=6,|F1F2|=![]() ,
,
若∠PF2F1为直角,则|PF1|2=|PF2|2+|F1F2|2,可解得:|PF1|=![]() ,|PF2|=
,|PF2|=![]() ,这时
,这时![]() .
.
若∠F2PF1为直角,则|PF1|2+|PF2|2=|F1F2|2,可解得:|PF1|=4,|PF2|=2,这时![]() .
.
解法2:由椭圆的对称性,不妨设P(x,y)(其中x>0,y>0),![]() .若∠PF2F1为直角,则P(
.若∠PF2F1为直角,则P(![]() ),这时|PF1|=
),这时|PF1|=![]() ,|PF2|=
,|PF2|=![]() ,这时
,这时![]() .若∠PF2F1为直角,则由
.若∠PF2F1为直角,则由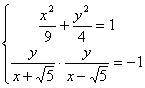 ,解得:
,解得:![]() .
.
于是|PF1|=4,|PF2|=2,这时![]() .
.
点评:由椭圆的方程,熟练准确地写出其几何性质(如顶点,焦点,长、短轴长,焦距,离心率,焦半径等)是应对考试必备的基本功;在解法2中设出了P点坐标的前提下,还可利用|PF1|=a+ex,|PF2|=a-ex来求解.
由已知,F1不是直角顶点,所以只要对P、F2中哪一个是直角顶点分两种情况即可.


科目:高中数学 来源: 题型:
| x2 |
| 4 |
| PF1 |
| PF2 |
| A、0 | B、2 | C、4 | D、-2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| ||
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 9 |
| y2 |
| 4 |
| |PF1| |
| |PF2| |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x2 |
| 4 |
| y2 |
| 3 |
| PF1 |
| PF2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com