
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的局部对称点.
的局部对称点.
(1)若![]() ,证明:函数
,证明:函数![]() 必有局部对称点;
必有局部对称点;
(2)若函数![]() 在区间
在区间![]() 内有局部对称点,求实数
内有局部对称点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上有局部对称点,求实数
上有局部对称点,求实数![]() 的取值范围.
的取值范围.
科目:高中数学 来源: 题型:
【题目】(本题满分12分) 如图,![]() 的外接圆
的外接圆![]() 的半径为
的半径为![]() ,
,![]() 所在的平面,
所在的平面,![]() ,
,![]() ,
,![]() ,且
,且![]() ,
,![]() .
.
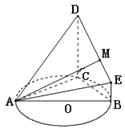
(1)求证:平面ADC![]() 平面BCDE.
平面BCDE.
(2)试问线段DE上是否存在点M,使得直线AM与平面ACD所成角的正弦值为![]() ?若存在,
?若存在,
确定点M的位置,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若点P是直线2x+y+10=0上的动点,直线PA、PB分别与圆x2+y2=4相切于A、B两点,则四边形PAOB(O为坐标原点)面积的最小值为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.

(1)求证:PA⊥BD;
(2)求证:平面BDE⊥平面PAC;
(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市10000名职业中学高三学生参加了一项综合技能测试,从中随机抽取100名学生的测试成绩,制作了以下的测试成绩![]() (满分是184分)的频率分布直方图.
(满分是184分)的频率分布直方图.
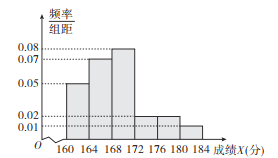
市教育局规定每个学生需要缴考试费100元.某企业根据这100000名职业中学高三学生综合技能测试成绩来招聘员工,划定的招聘录取分数线为172分,且补助已经被录取的学生每个人![]() 元的交通和餐补费.
元的交通和餐补费.
(1)已知甲、乙两名学生的测试成绩分别为168分和170分,求技能测试成绩![]() 的中位数,并对甲、乙的成绩作出客观的评价;
的中位数,并对甲、乙的成绩作出客观的评价;
(2)令![]() 表示每个学生的交费或获得交通和餐补费的代数和,把
表示每个学生的交费或获得交通和餐补费的代数和,把![]() 用
用![]() 的函数来表示,并根据频率分布直方图估计
的函数来表示,并根据频率分布直方图估计![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】[选修4-4:坐标系与参数方程]
已知动点![]() 都在曲线
都在曲线![]() (
(![]() 为参数,
为参数,![]() 是与
是与![]() 无关的正常数)上,对应参数分别为
无关的正常数)上,对应参数分别为![]() 与
与![]() ,
,![]() 为
为![]() 的中点.
的中点.
(1)求![]() 的轨迹的参数方程;
的轨迹的参数方程;
(2)作一个伸压变换:![]() ,求出动点
,求出动点![]() 点的参数方程,并判断动点
点的参数方程,并判断动点![]() 的轨迹能否过点
的轨迹能否过点![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班同学利用国庆节假期进行社会实践,在![]() 年龄段的人群中随机抽取
年龄段的人群中随机抽取![]() 人进行了一次生活习惯是否符合低碳观念的调查,生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数的频率分布直方图:
人进行了一次生活习惯是否符合低碳观念的调查,生活习惯符合低碳观念的称为“低碳族”,否则称为“非低碳族”,得到如下统计表和各年龄段人数的频率分布直方图:
组别 | 分组 | “低碳族”的人数 | 占本组的频率 |
第1组 |
| 120 | 0.6 |
第2组 |
| 195 |
|
第3组 |
| 100 | 0.5 |
第4组 |
|
| 0.4 |
第5组 |
| 30 | 0.3 |
第6组 |
| 15 | 0.3 |
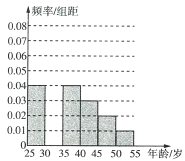
(1)补全频率分布直方图,并求![]() ,
,![]() ,
,![]() 的值;
的值;
(2)从![]() 年龄段的“低碳族”中采用分层随机抽样的方法抽取6人,求从
年龄段的“低碳族”中采用分层随机抽样的方法抽取6人,求从![]() 年龄段的“低碳族”中应抽取的人数.
年龄段的“低碳族”中应抽取的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)从某厂生产的一批零件1000个中抽取20个进行研究,应采用什么抽样方法?
(2)对(1)中的20个零件的直径进行测量,得到下列不完整的频率分布表:(单位:mm)
分组 | 频数 | 频率 |
| 2 | |
| 6 | |
| 8 | |
| ||
合计 | 20 | 1 |
①完成频率分布表;
②画出其频率分布直方图.
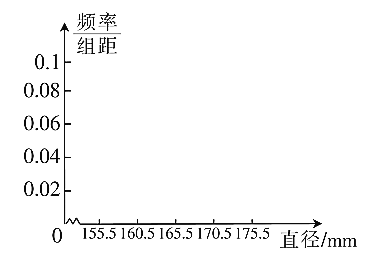
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线 y = x3 + x-2 在点 P0 处的切线![]() 平行于直线
平行于直线
4x-y-1=0,且点 P0 在第三象限,
⑴求P0的坐标;
⑵若直线![]() , 且 l 也过切点P0 ,求直线l的方程.
, 且 l 也过切点P0 ,求直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com