
 a+1)(a2-
a+1)(a2- a+1)与(a2+a+1)(a2-a+1)的大小.
a+1)与(a2+a+1)(a2-a+1)的大小.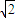 a+1)(a2-
a+1)(a2-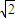 a+1)-(a2+a+1)(a2-a+1)等于-a2,再由a≠0,可得(a2+
a+1)-(a2+a+1)(a2-a+1)等于-a2,再由a≠0,可得(a2+ a+1)(a2-
a+1)(a2-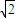 a+1)-(a2+a+1)(a2-a+1)<0,从而得出结论.
a+1)-(a2+a+1)(a2-a+1)<0,从而得出结论. a+1)(a2-
a+1)(a2-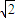 a+1)=(a2+1)2 -
a+1)=(a2+1)2 -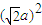 ,
,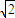 a+1)(a2-
a+1)(a2-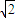 a+1)-(a2+a+1)(a2-a+1)=[(a2+1)2-
a+1)-(a2+a+1)(a2-a+1)=[(a2+1)2-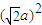 ]-[(a2+1)2-a2]
]-[(a2+1)2-a2] a+1)(a2-
a+1)(a2- a+1)<(a2+a+1)(a2-a+1).
a+1)<(a2+a+1)(a2-a+1).

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com