设函数f(x)=(1+x)2-2ln(1+x)
(1)若定义域内存在x,使得不等式f(x)-m≤0成立,求实数m的最小值;
(2)g(x)=f(x)-x2-x-a在区间[0,3]上恰有两个不同的零点,求a范围.
【答案】
分析:(1)存在x
,使m≥f(x
)
min,故
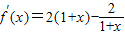
,由此导出f(x
)
min=f(0)=1,从而能够求出实数m的最小值.
(2)由g(x)=f(x)-x
2-x-a在区间[0,3]上恰有两个不同的零点,知x+1-2ln(1+x)=a有两个交点,令h(x)=x+1-2ln(1+x),
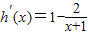
=
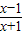
,由此利用函数的单调性能够求出a的取值范围.
解答:解:(1)存在x
,使m≥f(x
)
min,
∵f(x)=(1+x)
2-2ln(1+x),
∴
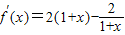
=
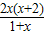
,x>-1.
令f′(x)>0,得x>0,
令f′(x)<0,得x<0,
∴y=f(x)在(-1,0)上单调递减,在(0,+∞)上单调递增,
∴f(x
)
min=f(0)=1,
∴m≥1,
∴实数m的最小值是1.
(2)∵g(x)=f(x)-x
2-x-a在区间[0,3]上恰有两个不同的零点,
∴g(x)=x+1-a-2ln(1+x)在区间[0,3]上恰有两个不同的零点,
∴x+1-2ln(1+x)=a有两个交点,
令h(x)=x+1-2ln(1+x),
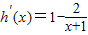
=
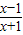
,
由h′(x)>0,得x>1,
由h′(x)<0,得x<1,
∴y=f(x)在[0,1]上单调递减,在[1,3]上单调递增,
∵h(0)=1-2ln1=1,
h(1)=2-2ln2,
h(3)=4-2ln4,
∴2-2ln2<a≤1.
点评:本题考查利用导数求闭区间上函数最值的应用,解题时要认真审题,仔细解答,注意等价转化思想的合理运用.

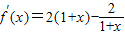 ,由此导出f(x)min=f(0)=1,从而能够求出实数m的最小值.
,由此导出f(x)min=f(0)=1,从而能够求出实数m的最小值.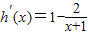 =
=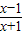 ,由此利用函数的单调性能够求出a的取值范围.
,由此利用函数的单调性能够求出a的取值范围.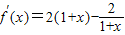
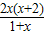 ,x>-1.
,x>-1.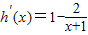 =
=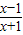 ,
,

 走进文言文系列答案
走进文言文系列答案