
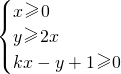 表示的平面区域是一个直角三角形,则该三角形的面积为
表示的平面区域是一个直角三角形,则该三角形的面积为
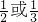
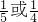
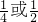
 ,从而得到三角形三个顶点的坐标,求出面积为
,从而得到三角形三个顶点的坐标,求出面积为 ;(2)直线x=0与直线kx-y+1=0互相垂直,可得k=0,从而得到三角形三个顶点的坐标,求出面积为
;(2)直线x=0与直线kx-y+1=0互相垂直,可得k=0,从而得到三角形三个顶点的坐标,求出面积为 .
.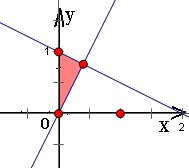
 ,y=2x与-
,y=2x与- x-y+1=0的交点坐标为(
x-y+1=0的交点坐标为(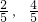 ),
),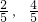 ),
), ×1×
×1× =
= ;
;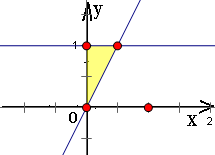
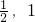 )
)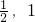 ),
), ×1×
×1× =
= .
. 或
或


 口算能手系列答案
口算能手系列答案科目:高中数学 来源: 题型:单选题
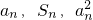 成等差数列,设数列{bn}的前n项和为Tn,且
成等差数列,设数列{bn}的前n项和为Tn,且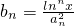 ,则对任意的实数x∈(1,e](e是自然对数的底)和任意正整数n,Tn小于的最小正整数为
,则对任意的实数x∈(1,e](e是自然对数的底)和任意正整数n,Tn小于的最小正整数为查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
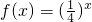 ,又函数g(x)=|xsinπx|,则函数h(x)=f(x)-g(x)在
,又函数g(x)=|xsinπx|,则函数h(x)=f(x)-g(x)在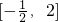 上的零点个数为
上的零点个数为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com