
 ,求AC的长.
,求AC的长.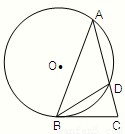
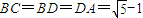 ,由切割线定理知BC2=CD•CA,解方程求得AC的长.
,由切割线定理知BC2=CD•CA,解方程求得AC的长.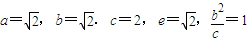 ,分M在双曲线的左支上和M在双曲线的右支上两种情况,利用双曲线的定义求得ρ与θ的关系式.
,分M在双曲线的左支上和M在双曲线的右支上两种情况,利用双曲线的定义求得ρ与θ的关系式.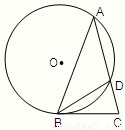 解:(1)如图,由∠C=72°,AB=AC知,∠ABC=72°,∠BAC=36°.
解:(1)如图,由∠C=72°,AB=AC知,∠ABC=72°,∠BAC=36°.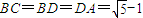 ,…(8分)
,…(8分)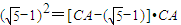 ,
,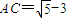 (舍),所以AC的长为2.…(12分)
(舍),所以AC的长为2.…(12分)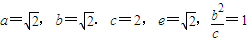 ,结合图形,
,结合图形,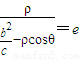 ,即
,即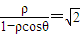 ,所以
,所以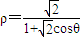 .(6分)
.(6分)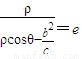 ,即
,即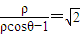 ,所以
,所以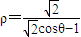 .(12)分
.(12)分

 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案科目:高中数学 来源: 题型:
 请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.
请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)
选做题(请考生在以下三个小题中任选一题作答,如果多做,则按所做的第一题评阅记分)| π |
| 4 |
| ||
| 2 |
| 2 |
| 2 |
| 1 |
| x |
查看答案和解析>>
科目:高中数学 来源:2010年本溪市高二下学期期末考试(理科)数学卷 题型:填空题
注意:请考生在(1)、(2)、(3)三题中任选一题做答,如果多做,则按所做的第一题计分
(1)如图,AC为⊙O的直径,弦BD⊥AC于点P,PC=2,PA=8,
则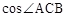 的值为 _____.
的值为 _____.

(2)在极坐标系中,圆 的圆心的极坐标是 _____.
的圆心的极坐标是 _____.
(3)不等式 的解集为 _____.
的解集为 _____.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
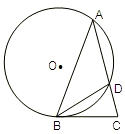 请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.
请考生在(1)(2)中任选一题作答,每小题12分.如都做,按所做的第(1)题计分.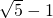 ,求AC的长.
,求AC的长.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com