
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]()
![]() 的右焦点为
的右焦点为![]() ,上顶点为
,上顶点为![]() ,
,![]() ,点
,点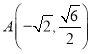 在椭圆
在椭圆![]() 上.
上.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)动直线l与椭圆![]() 相交于
相交于![]() 、
、![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴的正半轴相交于点
轴的正半轴相交于点![]() ,
,![]() 为线段
为线段![]() 的中点,若
的中点,若![]() 为定值
为定值![]() ,请判断直线l是否过定点,求实数
,请判断直线l是否过定点,求实数![]() 的值,并说明理由.
的值,并说明理由.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】在抗击新冠肺炎的疫情中,某医院从3位女医生,5位男医生中选出4人参加援鄂医疗队,至少有一位女医生入选,其中女医生甲和男医生乙不能同时参加,则不同的选法共有种______(用数字填写答案).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线![]() 经过点
经过点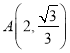 ,两个焦点为
,两个焦点为![]() ,
,![]() .
.
(1)求![]() 的方程;
的方程;
(2)设![]() 是
是![]() 上一点,直线
上一点,直线![]() 与直线
与直线![]() 相交于点
相交于点![]() ,与直线
,与直线![]() 相交于点
相交于点![]() ,证明:当
,证明:当![]() 点在
点在![]() 上移动时,
上移动时,![]() 为定值,并求此定值.
为定值,并求此定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下面给出有关![]() 的四个论断:①
的四个论断:①![]() ;②
;②![]() ;③
;③![]() 或
或![]() ;④
;④![]() .以其中的三个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:若______,则_______(用序号表示)并给出证明过程:
.以其中的三个论断作为条件,余下的一个论断作为结论,写出一个正确的命题:若______,则_______(用序号表示)并给出证明过程:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,某区有一块空地![]() ,其中
,其中![]() ,
,![]() ,
,![]() .当地区政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖
.当地区政府规划将这块空地改造成一个旅游景点,拟在中间挖一个人工湖![]() ,其中
,其中![]() 都在边
都在边![]() 上,且
上,且![]() ,挖出的泥土堆放在
,挖出的泥土堆放在![]() 地带上形成假山,剩下的
地带上形成假山,剩下的![]() 地带开设儿童游乐场.为安全起见,需在
地带开设儿童游乐场.为安全起见,需在![]() 的周围安装防护网.
的周围安装防护网.

(1)当![]() 时,求防护网的总长度;
时,求防护网的总长度;
(2)若要求挖人工湖用地![]() 的面积是堆假山用地
的面积是堆假山用地![]() 的面积的
的面积的![]() 倍,试确定
倍,试确定![]() 的大小;
的大小;
(3)为节省投入资金,人工湖![]() 的面积要尽可能小,问如何设计施工方案,可使
的面积要尽可能小,问如何设计施工方案,可使![]() 的面积最小?最小面积是多少?
的面积最小?最小面积是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某化工厂引进一条先进生产线生产某种化工产品,其生产的总成本![]() (万元)与年产量
(万元)与年产量![]() (吨)之间的函数关系式可以近似的表示为
(吨)之间的函数关系式可以近似的表示为![]() ,已知此生产线年产量最大为
,已知此生产线年产量最大为![]() 吨.
吨.
(1)求年产量为多少吨时,生产每吨产品的平均成本最低,并求最低成本;
(2)若每吨产品平均出厂价为40万元,那么当年产量为多少吨时,可以获得最大利润?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com