【题目】已知函数，.

（Ⅰ）若，解不等式；

（Ⅱ）若不等式至少有一个负数解，求实数的取值范围.

参考答案：

【答案】（Ⅰ）{x|1≤x≤0}．（Ⅱ）( ，2)．

【解析】【试题分析】(I)当时,利用零点分段法去绝对值,将不等式变为分段不等式来求得解集.(II)作出函数的图象和函数的图象,通过数形结合与分类讨论的数学思想方法求得的取值范围.

【试题解析】

（Ⅰ）若a=1，则不等式+≥3化为2+|x1|≥3．

当x≥1时，2+x1≥3，即x+2≤0，(x )2+ ≤0不成立；

当x<1时，2x+1≥3，即+x≤0，解得1≤x≤0．

综上，不等式+≥3的解集为{x|1≤x≤0}．

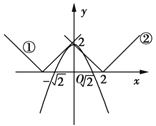
（Ⅱ）作出y=的图象如图所示，当a<0时，的图象如折线①所示，

由，得+xa2=0，若相切，则Δ=1+4(a+2)=0，得a= ，

数形结合知，当a≤ 时，不等式无负数解，则 <a<0．

当a=0时，满足>至少有一个负数解．

当a>0时，的图象如折线②所示，

此时当a=2时恰好无负数解，数形结合知，

当a≥2时，不等式无负数解，则0<a<2．

综上所述，若不等式>至少有一个负数解，

则实数a的取值范围是( ，2)．

关闭