
【题目】设数列{an}的前n项和为Sn . 若Sn=2an﹣n,则 ![]() +
+ ![]() +
+ ![]() +
+ ![]() = .
= .
【答案】![]()
【解析】解:∵Sn=2an﹣n,∴n≥2时,an=Sn﹣Sn﹣1=2an﹣n﹣[2an﹣1﹣(n﹣1)],∴an=2an﹣1+1,化为:an+1=2(an﹣1+1),
n=1时,a1=2a1﹣1,解得a1=1.
∴数列{an+1}是等比数列,首项为2,公比为2.
∴an+1=2n,即an=2n﹣1,
∴ ![]() =
= ![]() =
= ![]() .
.
∴ ![]() +
+ ![]() +
+ ![]() +
+ ![]() =
= ![]() +
+ ![]() +…+
+…+ ![]() =1﹣
=1﹣ ![]() =
= ![]() .
.
故答案为: ![]() .
.
Sn=2an﹣n,n≥2时,an=Sn﹣Sn﹣1,化为:an+1=2(an﹣1+1),n=1时,a1=2a1﹣1,解得a1.利用等比数列的通项公式可得an=2n﹣1,于是 ![]() =
= ![]() =
= ![]() .利用裂项求和方法即可得出.
.利用裂项求和方法即可得出.


科目:高中数学 来源: 题型:
【题目】下列几个命题正确的个数是( )
①若方程![]() 有一个正实根,一个负实根,则
有一个正实根,一个负实根,则![]() ;
;
②函数![]() 是偶函数,但不是奇函数;
是偶函数,但不是奇函数;
③设函数![]() 的定义域为
的定义域为![]() ,则函数
,则函数![]() 与函数
与函数![]() 图像关于
图像关于![]() 轴对称;
轴对称;
④一条曲线![]() 和直线
和直线![]() 的公共点个数是
的公共点个数是![]() ,则
,则![]() 的值不可能是1。
的值不可能是1。
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l:x+2y-2=0,试求:
(1)点P(-2,-1)关于直线l的对称点坐标;
(2)直线![]() 关于直线l对称的直线l2的方程;
关于直线l对称的直线l2的方程;
(3)直线l关于点(1,1)对称的直线方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ﹣
﹣ ![]() =1(a>0,b>0)的左、右焦点分别为F1、F2 , 过右焦点F2且与x轴垂直的直线与双曲线两条渐近线分别交于A,B两点,若△ABF1为等腰直角三角形,且|AB|=4
=1(a>0,b>0)的左、右焦点分别为F1、F2 , 过右焦点F2且与x轴垂直的直线与双曲线两条渐近线分别交于A,B两点,若△ABF1为等腰直角三角形,且|AB|=4 ![]() ,P(x,y)在双曲线上,M(
,P(x,y)在双曲线上,M( ![]() ,
, ![]() ),则|PM|+|PF2|的最小值为( )
),则|PM|+|PF2|的最小值为( )
A.![]() ﹣1
﹣1
B.2
C.2 ![]() ﹣2
﹣2
D.3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2017x+sin2017x,g(x)=log2017x+2017x , 则( )
A.对于任意正实数x恒有f(x)≥g(x)
B.存在实数x0 , 当x>x0时,恒有f(x)>g(x)
C.对于任意正实数x恒有f(x)≤g(x)
D.存在实数x0 , 当x>x0时,恒有f(x)<g(x)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一个圆柱形圆木的底面半径为1 m,长为10 m,将此圆木沿轴所在的平面剖成两部分.现要把其中一部分加工成直四棱柱木梁,长度保持不变,底面为等腰梯形ABCD(如图所示,其中O为圆心,C,D在半圆上),设![]() ,木梁的体积为V(单位:m3),表面积为S(单位:m2).
,木梁的体积为V(单位:m3),表面积为S(单位:m2).
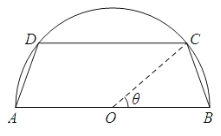
(1)求V关于θ的函数表达式;
(2)求![]() 的值,使体积V最大;
的值,使体积V最大;
(3)问当木梁的体积V最大时,其表面积S是否也最大?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】端午节小长假期间,张洋与几位同学从天津乘火车到大连去旅游,若当天从天津到大连的三列火车正点到达的概率分别为0.8,0.7,0.9,假设这三列火车之间是否正点到达互不影响,则这三列火车恰好有两列正点到达的概率是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com