练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    如图，为处理含有某种杂质的污水，要制造一底宽为2米的无盖长方体沉淀箱，污水从孔流入，经沉淀后从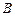孔流出，设箱体的长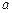为米，高为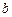米．已知流出的水中该杂质的质量分数与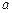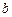，的乘积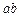成反比，现有制箱材料60平方米，问当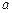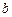，各为多少米时，经沉淀后流出的水中该杂质的质量分数最小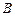（，孔的面积忽略不计）．
    当为6米，为3米时，经沉淀后流出的水中该杂质的质量分数最小
    设为流出的水中杂质的质量分数，则，
    其中为比例系数，依题意，即所求的，值使值最小，根据题设，有得．
    于是．
    当时，或（舍去）．
    本题只有一个极值点，
    当时，，
    即当为6米，为3米时，经沉淀后流出的水中该杂质的质量分数最小．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：不详 题型：解答题

    若a、b、c都是正数，且a+b+c=1，
    求证： (1–a)(1–b)(1–c)≥8abc

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    某公司一年需要一种计算机元件8000个，每天需同样多的元件用于组装整机，该元件每年分n次进货，每次购买元件的数量均为x，购一次货需手续费500元．已购进而未使用的元件要付库存费，假设平均库存量为件，每个元件的库存费为每年2元，如果不计其他费用，请你帮公司计算，每年进货几次花费最小？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    （1）已知x＞0,y＞0，且+=1,求x+y的最小值；
    （2）已知x＜,求函数y=4x-2+的最大值；
    （3）若x,y∈(0,+∞)且2x+8y-xy=0，求x+y的最小值.

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

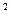    某单位建造一间背面靠墙的小房，地面面积为12 m，房屋正面每平方米的造价为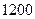元，房屋侧面每平方米的造价为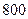元，屋顶的造价为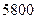元．如果墙高为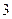m，且不计房屋背面和地面的费用，问怎样设计房屋能使总等价最低？最低总造价是多少？

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：解答题

    已知，求的最小值

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：填空题

    设x，y，z为正实数，x－2y＋3z＝0，则的最小值是       

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    已知两个正数、满足，当取得最小值时，、的值分别为(      )
    A． 5、5B． 10、C． 10、5D． 10、10

    查看答案和解析>>

    科目：高中数学 来源：不详 题型：单选题

    设不等的两个正数满足，则的取值范围是（    ）
    A．B．
    C．D．

    查看答案和解析>>

    同步练习册答案