
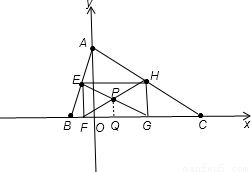
 解:①当E、H分别为|AB|和|AC|的中点时,
解:①当E、H分别为|AB|和|AC|的中点时,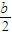 ,
,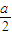 ),F(
),F(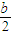 ,0),H(
,0),H(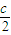 ,
,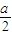 ),G(
),G(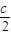 ,0)
,0)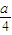 ,|FQ|=
,|FQ|= |EH|=
|EH|= |BC|=
|BC|= (c-b),
(c-b), ,所以|OQ|=|FQ|-|OF|=
,所以|OQ|=|FQ|-|OF|= (c-b)+
(c-b)+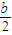 =
=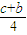 ,所以P(
,所以P(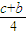 ,
,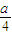 );
);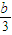 ,
,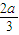 ),F(
),F(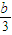 ,0),H(
,0),H(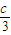 ,
,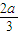 ),G(
),G(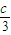 ,0)
,0) ,|FQ|=
,|FQ|= |EH|=
|EH|= |BC|=
|BC|= (c-b),而|FO|=-
(c-b),而|FO|=-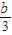 ,
, (c-b)+
(c-b)+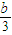 =
=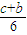 ,所以P′(
,所以P′(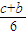 ,
,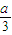 ).
).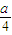 =
=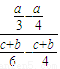 (x-
(x-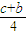 ),化简得y=
),化简得y=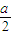 -
-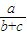 x
x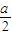 -
-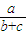 x
x

科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| RP |
| PN |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2011年江苏省淮安市洪泽中学高考数学模拟试卷(3)(解析版) 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com