
| �� | ���� | �ϼ� | |
| ��ְ�� | 22 | 8 | 30 |
| Ůְ�� | 8 | 12 | 20 |
| �ϼ� | 30 | 20 | 50 |
| P��K2��k�� | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
���� ��1�����ݷֲ�����Ķ��彨��������ϵ���ɵõ����ۣ�
��2�������оٷ�������������һ����ְ���ĸ��ʣ�
��3������K2����϶����Լ�������жϣ�
��� �⣺��1���ڲ��ɵ�ְ���г�5�ˣ����ȡ����Ϊ$\frac{5}{20}$=$\frac{1}{4}$��
������ְ��Ӧ�ó�ȡ8��$\frac{1}{4}$=2���ˣ���Ůְ��Ӧ�ó�ȡ12��$\frac{1}{4}$=3���ˣ���
��2��������ȡ��5���У���ְ��2�˼�Ϊa��b��Ůְ��4�˼�Ϊc��d��e�����5����ѡ2�˵��������Ϊ��a��b������a��c������a��d������a��e������b��c������b��d������b��e������c��d������c��e������d��e������10�������
����������һ����ְ��������У�a��b������a��c������a��d������a��e������b��c������b��d������b��e������7�������
�ʴ�������ȡ��5����ѡ2�ˣ�������һ����ְ���ĸ���ΪP=$\frac{7}{10}$��
��3����ΪK2=$\frac{50����22��12-8��8��2}{30��20��30��20}$��5.56�ʣ�3.841��6.635����
������95%�İ�����Ϊ���Լ�����ѵ��̬�����Ա��йء���
���� ������Ҫ�����ۺϿ�������Լ��飬�ֲ�����Լ����ʵ���⣬����ѧ�������������������


 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д� ����ѧУ�ֲ����ܲ�ϵ�д�
����ѧУ�ֲ����ܲ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-$\sqrt{2}$��$\sqrt{2}$] | B�� | {-$\sqrt{2}$��$\sqrt{2}$} | C�� | ��-$\sqrt{2}$��$\sqrt{2}$�� | D�� | [0��$\sqrt{2}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{4}{3}$ | B�� | 1+$\sqrt{3}$ | C�� | 1 | D�� | $\frac{1+\sqrt{3}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
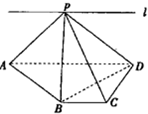 ��ͼ��ABCDΪֱ�����Σ���C=��CDA=90�㣬AD=2BC=2CD=2��PΪƽ��ABCD��һ�㣬��PB��BD��
��ͼ��ABCDΪֱ�����Σ���C=��CDA=90�㣬AD=2BC=2CD=2��PΪƽ��ABCD��һ�㣬��PB��BD���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\left\{{x|x=k��+\frac{��}{3}��k��z}\right\}$ | B�� | $\left\{{x|x=k��-\frac{��}{3}��k��z}\right\}$ | C�� | $\left\{{x|x=2k��\frac{��}{3}��k��z}\right\}$ | D�� | $\left\{{x|x=k��\frac{��}{3}��k��z}\right\}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 0 | B�� | 1 | C�� | 1-2ln2 | D�� | $\frac{-1+ln2}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com