
| A. | 0 | B. | 1 | C. | 1-2ln2 | D. | $\frac{-1+ln2}{2}$ |
分析 问题转化为a${(\frac{1+lnx}{x}-1)}_{min}$对于任意$x∈[{\frac{1}{2},2}]$恒成立,设f(x)=$\frac{1+lnx}{x}$-1,求出函数f(x)的最小值即可求出a的最大值.
解答 解:(a+1)x-1-lnx≤0对于任意$x∈[{\frac{1}{2},2}]$恒成立
?a≤$\frac{1+lnx}{x}$-1对于任意$x∈[{\frac{1}{2},2}]$恒成立
?a≤${(\frac{1+lnx}{x}-1)}_{min}$对于任意$x∈[{\frac{1}{2},2}]$恒成立
设f(x)=$\frac{1+lnx}{x}$-1,$x∈[{\frac{1}{2},2}]$,则f′(x)=$\frac{-lnx}{{x}^{2}}$,
令f′(x)>0,解得:$\frac{1}{2}$≤x<1,令f′(x)>0,解得:1<x≤2,
∴f(x)在[$\frac{1}{2}$,1)递增,在(1,2]递减,
∴f($\frac{1}{2}$)或f(2)最小,
而f($\frac{1}{2}$)=1-2ln2,f(2)=$\frac{1}{2}$ln2-$\frac{1}{2}$,
∴f($\frac{1}{2}$)<f(2),
∴a的最大值是1-2ln2,
故选:C.
点评 本题考查函数恒成立问题,着重考查构造函数思想、等价转化思想与导数法求极值的综合应用,求得f(x)的最小值是关键,属于中档题


科目:高中数学 来源: 题型:选择题
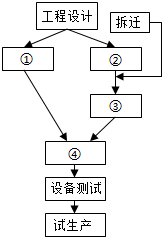 某公司要在某一规划区域内筹建工厂,拆迁与工程设计可同时进行,如果工程设计分为土建设计与设备采购两个部分,两者可同时进行;拆迁和土建设计进行完才能进行厂房建设,厂房建设和设备采购进行完才能进行设备安装调试,最后才能进行试生产.上述过程的工序流程图如图.则设备采购,厂房建设,土建设计,设备安装与图中①②③④处正确的对应次序应为( )
某公司要在某一规划区域内筹建工厂,拆迁与工程设计可同时进行,如果工程设计分为土建设计与设备采购两个部分,两者可同时进行;拆迁和土建设计进行完才能进行厂房建设,厂房建设和设备采购进行完才能进行设备安装调试,最后才能进行试生产.上述过程的工序流程图如图.则设备采购,厂房建设,土建设计,设备安装与图中①②③④处正确的对应次序应为( )| A. | ①②③④ | B. | ①④②③ | C. | ②③①④ | D. | ①③②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 赞成 | 不赞成 | 合计 | |
| 男职工 | 22 | 8 | 30 |
| 女职工 | 8 | 12 | 20 |
| 合计 | 30 | 20 | 50 |
| P(K2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 正方形ABCD与正方形ABEF互相垂直,点M,N,G分别是AE,BC,CE的中点,AB=2.
正方形ABCD与正方形ABEF互相垂直,点M,N,G分别是AE,BC,CE的中点,AB=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{2}{π}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
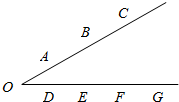 如图,A,B,C三点与D,E,F,G四点分别在一个以O为顶点的角的不同的两边上,则在A,B,C,D,E,F,G,O这8个点中任选三个点作为三角形的三个顶点,可构成的三角形的个数为42.
如图,A,B,C三点与D,E,F,G四点分别在一个以O为顶点的角的不同的两边上,则在A,B,C,D,E,F,G,O这8个点中任选三个点作为三角形的三个顶点,可构成的三角形的个数为42.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com