
已知圆C的方程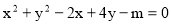
(1)若点 在圆C的内部,求m的取值范围;
在圆C的内部,求m的取值范围;
(2)若当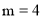 时
时
①设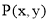 为圆C上的一个动点,求
为圆C上的一个动点,求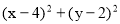 的最值;.
的最值;.
②问是否存在斜率是1的直线l,使l被圆C截得的弦AB,以AB为直径的圆经过原点,若存在,写出直线l的方程;若不存在,说明理由.
(1)m>-5 (2)①4 ②存在直线l,其方程为y=x-4或y=x+1
【解析】
试题分析:(1)根据圆C的标准方程可得m>-5.再根据点A(m,-2)在圆C的内部,可得  ,由此求得m的范围.
,由此求得m的范围.
(2)① 表示圆C上的点P(x,y)到点H(4,2)的距离的平方,求得|HC|=5,故
表示圆C上的点P(x,y)到点H(4,2)的距离的平方,求得|HC|=5,故 的最大值为HC加上半径后的平方,的最小值为HC减去半径后的平方.
的最大值为HC加上半径后的平方,的最小值为HC减去半径后的平方.
②假设存在直线l满足题设条件,设l的方程为y=x+m,则AB中点N是两直线x-y+m=0与y+2=-(x-1)的交点,即N(?),以AB为直径的圆经过原点,求得|AN|=,|ON|=,由|AN|=|ON|,解得m的值,可得结论.
试题解析:(1) ,∴m>-5.
,∴m>-5.
(2)①当m=4时,圆C的方程即 ,而
,而 表示圆C上的点P(x,y)到点H(4,2)的距离的平方,由于|HC|=
表示圆C上的点P(x,y)到点H(4,2)的距离的平方,由于|HC|= =5,故
=5,故 的最大值为 (5+3)2=64,
的最大值为 (5+3)2=64, 的最小值为 (5-3)2=4.
的最小值为 (5-3)2=4.
②法一:假设存在直线l满足题设条件,设l的方程为y=x+m,圆C化为 ,圆心C(1,-2),则AB中点N是两直线x-y+m=0与y+2=-(x-1)的交点即N
,圆心C(1,-2),则AB中点N是两直线x-y+m=0与y+2=-(x-1)的交点即N ,以AB为直径的圆经过原点,
,以AB为直径的圆经过原点,
∴|AN|=|ON|,又CN⊥AB,|CN|= ,
,
∴|AN|= .
.
又|ON|=
由|AN|=|ON|,解得m=-4或m=1.
∴存在直线l,其方程为y=x-4或y=x+1.
法二:假设存在直线l,设其方程为:
由
得: ①
①
设A( ),B(
),B( )
)
则: ∴
∴


又∵OA⊥OB
∴ ∴
∴
解得b=1或
把b=1和 分别代入①式,验证判别式均大于0,故存在b=1或
分别代入①式,验证判别式均大于0,故存在b=1或
∴存在满足条件的直线方程是:
考点:直线与圆的位置关系;点与圆的位置关系.


科目:高中数学 来源:2016届福建省高一下学期期中考试数学试卷(解析版) 题型:选择题
如图所示的程序框图是计算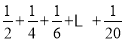 的值,其中判断框内应填入的条件是( )
的值,其中判断框内应填入的条件是( )
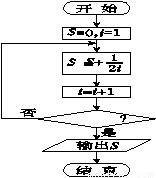
A.i >8 B.i >9 C.i >10 D.i >11
查看答案和解析>>
科目:高中数学 来源:2016届福建省高一下学期期中考试数学试卷(解析版) 题型:选择题
有50件产品,编号为0,1,2,…,49,现从中抽取5个进行检验,用系统抽样的方法抽取样本的编号可以为( )
A.5,10,15,20,25 B.5,13,21,29,37
C.8,22,23,1,20 D.1,11,21,31,41
查看答案和解析>>
科目:高中数学 来源:2016届福建省泉州市高一下学期期末考试数学试卷(解析版) 题型:解答题
已知直线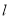
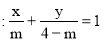
(1)若直线的斜率小于2,求实数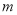 的取值范围;
的取值范围;
(2)若直线分别与x轴、y轴的正半轴交于A、B两点,O是坐标原点,求△AOB面积的最大值及此时直线的方程.
查看答案和解析>>
科目:高中数学 来源:2016届湖北省荆门市高一下学期期末质量检测数学试卷(解析版) 题型:填空题
如图,某海事部门举行安保海上安全演习.为了测量正在海面匀速行驶的某航船的速度,在海岸上选取距离为1千米的两个观察点C,D,在某天10:00观察到该航船在A处,此时测得∠ADC=30°,3分钟后该船行驶至B处,此时测得∠ACB=60°,∠BCD=45°,∠ADB=60°,则船速为 千米/分钟.(用含根号的式子表示)
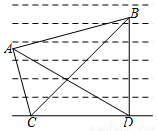
查看答案和解析>>
科目:高中数学 来源:[同步]2014年北师大版选修1-2 1.2独立性检验练习卷(解析版) 题型:填空题
(2012•佛山二模)抛掷一枚质地均匀的骰子,所得点数的样本空间为S={1,2,3,4,5,6},令事件A={2,3,5},事件B={1,2,4,5,6},则P(A|B)的值为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com