Question

11．过点P（-2，-1）作圆C：（x-4）²+（y-2）²=9的两条切线，切点分别为A，B，
（1）求直线AB的方程；
（2）求在经过点A，B的所有圆中，面积最小的圆的方程．

Answer 1

分析 （1）连结AC，BC，PC，记PC交AB于D，根据AB⊥CD求出直线斜率，再根据C到直线AB的距离，可得直线AB的方程；
（2）经过点A，B的所有圆中，面积最小的圆是以AB为直径的圆，进而得到答案．

解答 解：（1）如图，连结AC，BC，PC，记PC交AB于D，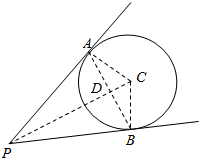

因为，PA，PB是圆C的切线，
所以CA⊥PA，CB⊥PB，PC⊥AB  …（2分）
在Rt△PAC中，PC=$3\sqrt{5}$，AC=3，∴PA=6
由Rt△PAC∽Rt△ADC得，$CD=\frac{3}{{\sqrt{5}}}$…（4分）
由条件知，圆心C（4，2），∴${k_{PC}}=\frac{1}{2}$，k_AB=-2
可设直线AB的方程为y=-2x+m，即2x+y-m=0，
∴$\frac{|10-m|}{{\sqrt{{2^2}+{1^2}}}}=\frac{3}{{\sqrt{5}}}$，∴m=7或m=13（舍去）
所以，直线AB的方程为y=-2x+7…（7分）
（2）在经过点A，B的所有圆中，以AB为直径的圆，其面积最小．…（9分）
直线PC的方程为x-2y=0，与y=-2x+7联立，
解得点D的坐标为$（\frac{14}{5}，\frac{7}{5}）$…（11分）
由（1）知，$AD=2CD=\frac{6}{{\sqrt{5}}}$…（13分）
∴所求圆的方程为：${（x-\frac{14}{5}）^2}+{（y-\frac{7}{5}）^2}=\frac{36}{5}$…（15分）

点评 本题考查的知识点是圆的切线方程，圆的标准方程，点到直线的距离公式，难度中档．