
已知函数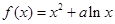 的图象在点
的图象在点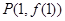 处的切线斜率为
处的切线斜率为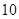 .
.
(Ⅰ)求实数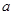 的值;
的值;
(Ⅱ)判断方程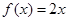 根的个数,证明你的结论;
根的个数,证明你的结论;
(Ⅲ)探究:是否存在这样的点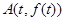 ,使得曲线
,使得曲线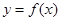 在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
在该点附近的左、右的两部分分别位于曲线在该点处切线的两侧?若存在,求出点A的坐标;若不存在,说明理由.
(1)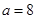
(2)方程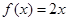 有且只有一个实根.
有且只有一个实根.
(3)存在唯一点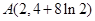 使得曲线在点
使得曲线在点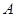 附近的左、右两部分分别
附近的左、右两部分分别
位于曲线在该点处切线的两侧.
【解析】
试题分析:解法一:(Ⅰ)因为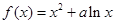 ,所以
,所以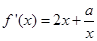 ,
,
函数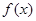 的图象在点
的图象在点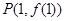 处的切线斜率
处的切线斜率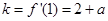 .
.
由 得:
得: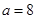 . 4分
. 4分
(Ⅱ)由(Ⅰ)知,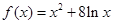 ,令
,令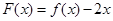
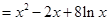 .
.
因为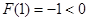 ,
,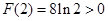 ,所以
,所以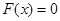 在
在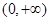 至少有一个根.
至少有一个根.
又因为 ,所以
,所以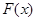 在
在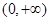 上递增,
上递增,
所以函数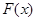 在
在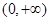 上有且只有一个零点,即方程
上有且只有一个零点,即方程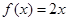 有且只有一
有且只有一
个实根. 7分
(Ⅲ)证明如下:
由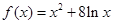 ,
,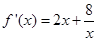 ,可求得曲线
,可求得曲线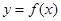 在点
在点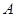 处的切
处的切
线方程为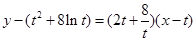 ,
,
即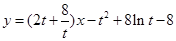
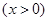 .
8分
.
8分
记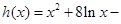
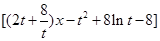
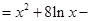
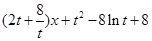
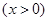 ,
,
则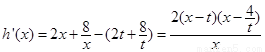 .
11分
.
11分
(1)当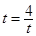 ,即
,即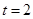 时,
时, 对一切
对一切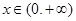 成立,
成立,
所以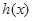 在
在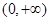 上递增.
上递增.
又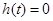 ,所以当
,所以当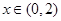 时
时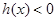 ,当
,当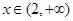 时
时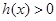 ,
,
即存在点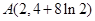 ,使得曲线在点A附近的左、右两部分分别位于曲线
,使得曲线在点A附近的左、右两部分分别位于曲线
在该点处切线的两侧. 12分
(2)当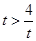 ,即
,即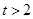 时,
时,
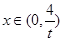 时,
时,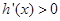 ;
;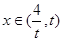 时,
时,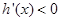 ;
;
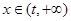 时,
时,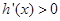 .
.
故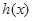 在
在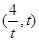 上单调递减,在
上单调递减,在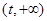 上单调递增.
上单调递增.
又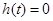 ,所以当
,所以当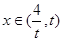 时,
时,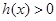 ;当
;当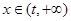 时,
时,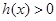 ,
,
即曲线在点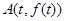 附近的左、右两部分都位于曲线在该点处切线的
附近的左、右两部分都位于曲线在该点处切线的
同侧. 13分
(3)当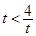 ,即
,即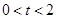 时,
时,
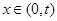 时,
时,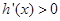 ;
;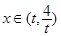 时,
时,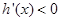 ;
;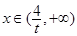 时,
时,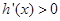 .
.
故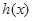 在
在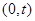 上单调递增,在
上单调递增,在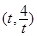 上单调递减.
上单调递减.
又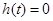 ,所以当
,所以当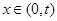 时,
时,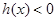 ;当
;当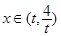 时,
时,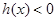 ,
,
即曲线在点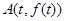 附近的左、右两部分都位于曲线在该点处切线的同侧.
附近的左、右两部分都位于曲线在该点处切线的同侧.
综上,存在唯一点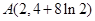 使得曲线在点
使得曲线在点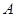 附近的左、右两部分分别
附近的左、右两部分分别
位于曲线在该点处切线的两侧. 14分
解法二:(Ⅰ)(Ⅱ)同解法一;
(Ⅲ)证明如下:
由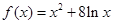 ,
,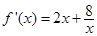 ,可求得曲线
,可求得曲线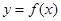 在点
在点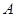 处的切
处的切
线方程为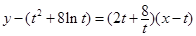 ,
,
即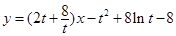
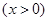 .
8分
.
8分
记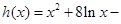
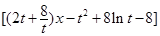
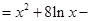
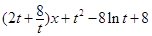
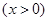 ,
,
则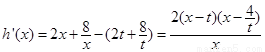 .
11分
.
11分
若存在这样的点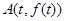 ,使得曲线
,使得曲线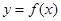 在该点附近的左、右两部分都
在该点附近的左、右两部分都
位于曲线在该点处切线的两侧,则问题等价于t不是极值点,
由二次函数的性质知,当且仅当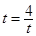 ,即
,即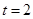 时,
时,
t不是极值点,即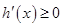 .
.
所以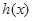 在
在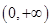 上递增.
上递增.
又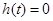 ,所以当
,所以当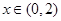 时,
时,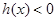 ;当
;当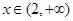 时,
时,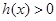 ,
,
即存在唯一点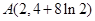 ,使得曲线在点
,使得曲线在点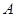 附近的左、右两部分分别
附近的左、右两部分分别
位于曲线在该点处切线的两侧. 14分
考点:函数、导数
点评:本题主要考查函数、导数等基础知识,考查推理论证能力、运算求解能力,函数与方程思想、数形结合思想、考查化归与转化思想.


科目:高中数学 来源:2013届山西省高二第二学期3月月考理科数学试卷 题型:选择题
已知函数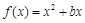 的图象在点
的图象在点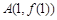 处的切线的斜率为3,数列
处的切线的斜率为3,数列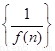
的前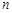 项和为
项和为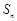 ,则
,则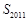 的值为( )
的值为( )
A、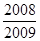 B、
B、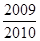 C、
C、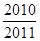 D、
D、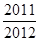
查看答案和解析>>
科目:高中数学 来源:2010年福建省八县(市高二下学期期末联考(文科)数学卷 题型:解答题
(本题满分14分)已知函数 的图象在点
的图象在点 处的切线的斜率为
处的切线的斜率为 ,且在
,且在 处取得极小值。
处取得极小值。
(1)求 的解析式;
的解析式;
(2)已知函数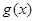 定义域为实数集
定义域为实数集 ,若存在区间
,若存在区间 ,使得
,使得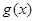 在
在 的值域也是
的值域也是 ,称区间
,称区间 为函数
为函数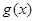 的“保值区间”.
的“保值区间”.
①当 时,请写出函数
时,请写出函数 的一个“保值区间”(不必证明);
的一个“保值区间”(不必证明);
②当 时,问
时,问 是否存在“保值区间”?若存在,写出一个“保值区间”并给予证明;若不存在,请说明理由.
是否存在“保值区间”?若存在,写出一个“保值区间”并给予证明;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com