
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,连接BM,MN,BN.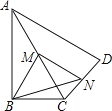
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
【答案】
(1)
证明:在△CAD中,∵M、N分别是AC、CD的中点,
∴MN∥AD,MN= ![]() AD,
AD,
在RT△ABC中,∵M是AC中点,
∴BM= ![]() AC,
AC,
∵AC=AD,
∴MN=BM.
(2)
解:∵∠BAD=60°,AC平分∠BAD,
∴∠BAC=∠DAC=30°,
由(1)可知,BM= ![]() AC=AM=MC,
AC=AM=MC,
∴∠BMC=∠BAM+∠ABM=2∠BAM=60°,
∵MN∥AD,
∴∠NMC=∠DAC=30°,
∴∠BMN=∠BMC+∠NMC=90°,
∴BN2=BM2+MN2,
由(1)可知MN=BM= ![]() AC=1,
AC=1,
∴BN= ![]()
【解析】(1)根据三角形中位线定理得MN= ![]() AD,根据直角三角形斜边中线定理得BM=
AD,根据直角三角形斜边中线定理得BM= ![]() AC,由此即可证明.(2)首先证明∠BMN=90°,根据BN2=BM2+MN2即可解决问题.
AC,由此即可证明.(2)首先证明∠BMN=90°,根据BN2=BM2+MN2即可解决问题.
【考点精析】利用直角三角形斜边上的中线和勾股定理的概念对题目进行判断即可得到答案,需要熟知直角三角形斜边上的中线等于斜边的一半;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:高中数学 来源: 题型:
【题目】已知△ABC是等腰三角形,AB=AC.
(1)特殊情形:如图1,当DE∥BC时,有DBEC.(填“>”,“<”或“=”)
(2)发现探究:若将图1中的△ADE绕点A顺时针旋转α(0°<α<180°)到图2位置,则(1)中的结论还成立吗?若成立,请给予证明;若不成立,请说明理由.
(3)拓展运用:如图3,P是等腰直角三角形ABC内一点,∠ACB=90°,且PB=1,PC=2,PA=3,求∠BPC的度数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按照国家环保部发布的新修订的《环境空气质量标准》,规定:PM2.5的年平均浓度不得超过35微克/立方米,国家环保部门在2016年10月1日到2017年1月30日这120天对全国的PM2.5平均浓度的监测数据统计如下:
组别 | PM2.5浓度(微克/立方米) | 频数(天) |
第一组 |
| 32 |
第二组 |
| 64 |
第三组 |
| 16 |
第四组 | 115以上 | 8 |
(1)在这120天中抽取30天的数据做进一步分析,每一组应抽取多少天?
(2)在(1)中所抽取的样本PM2.5的平均浓度超过75(微克/立方米)的若干天中,随机抽取2天,求恰好有一天平均浓度超过115(微克/立方米)的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,F为弦AC的中点,连接OF并延长交 ![]() 于点D,过点D作⊙O的切线,交BA的延长线于点E.
于点D,过点D作⊙O的切线,交BA的延长线于点E.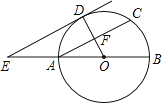
(1)求证:AC∥DE;
(2)连接CD,若OA=AE=a,写出求四边形ACDE面积的思路.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com