
【题目】如图,直三棱柱![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上.
上.

(Ⅰ)证明![]() ;
;
(Ⅱ)若![]() 是
是![]() 中点,证明
中点,证明![]() 平面
平面![]() ;
;
(Ⅲ)当![]() 时,求二面角
时,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() ,(Ⅰ)分别求出向量
,(Ⅰ)分别求出向量![]() 的坐标根据
的坐标根据![]() 可得结果;(Ⅱ)求出平面
可得结果;(Ⅱ)求出平面![]() 的法向量,利用向量法能证明
的法向量,利用向量法能证明![]() 平面
平面![]() ;(Ⅲ)求出平面
;(Ⅲ)求出平面![]() 的法向量和平面
的法向量和平面![]() 的法向量,利用空间向量法夹角余弦公式能求出二面角
的法向量,利用空间向量法夹角余弦公式能求出二面角![]() 的余弦值.
的余弦值.
试题解析:(Ⅰ)证明:如图,以![]() 为原点建立空间直角坐标系
为原点建立空间直角坐标系![]() .则
.则![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
![]() ,
,![]() ,
,
![]() ,所以
,所以![]() .
.

(Ⅱ)解法一:

![]()
设平面![]() 的法向量
的法向量![]() ,
,
由![]()
![]() ,
,
且![]()
![]() ,
,
令![]() 得
得![]() ,
,
所以![]() ,
,
又![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
解法二:证明:连接![]() ,交
,交![]() 于
于![]() ,
,![]() .
.
因为直三棱柱![]() ,
,![]() 是
是![]() 中点,
中点,
所以侧面![]() 为矩形,
为矩形,![]() 为
为![]() 的中位线.
的中位线.
所以![]() ,
,
因为![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
(Ⅲ)由(Ⅰ)知![]() ,
,
设![]() ,
,
因为点![]() 在线段
在线段![]() 上,且
上,且![]() ,即
,即![]()
![]()
![]() .
.
所以![]() ,
,![]() ,
,![]()
![]() .
.
所以![]() ,
,![]() .
.
平面![]() 的法向量为
的法向量为![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
由![]() ,
,![]() ,得
,得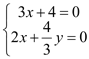 ,
,
所以![]() ,
,![]() ,
,![]()
![]() .
.
设二面角![]() 的大小为
的大小为![]() ,
,
所以 .
.
所以二面角![]() 的余弦值为
的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】己知圆![]() 的圆心在直线
的圆心在直线![]() 上,且过点
上,且过点![]() ,与直线
,与直线![]() 相切.
相切.
(![]() )求圆
)求圆![]() 的方程.
的方程.
(![]() )设直线
)设直线![]() 与圆
与圆![]() 相交于
相交于![]() ,
,![]() 两点.求实数
两点.求实数![]() 的取值范围.
的取值范围.
(![]() )在(
)在(![]() )的条件下,是否存在实数
)的条件下,是否存在实数![]() ,使得弦
,使得弦![]() 的垂直平分线
的垂直平分线![]() 过点
过点![]() ,若存在,求出实数
,若存在,求出实数![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥S-ABCD中,底面ABCD为菱形,SD⊥平面ABCD,点E为SD的中点.
(1)求证:直线SB∥平面ACE
(2)求证:直线AC⊥平面SBD.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“五一”假期期间,某餐厅对选择![]() 、
、![]() 、
、![]() 三种套餐的顾客进行优惠。对选择
三种套餐的顾客进行优惠。对选择![]() 、
、![]() 套餐的顾客都优惠10元,对选择
套餐的顾客都优惠10元,对选择![]() 套餐的顾客优惠20元。根据以往“五一”假期期间100名顾客对选择
套餐的顾客优惠20元。根据以往“五一”假期期间100名顾客对选择![]() 、
、![]() 、
、![]() 三种套餐的情况得到下表:
三种套餐的情况得到下表:
选择套餐种类 |
|
|
|
选择每种套餐的人数 | 50 | 25 | 25 |
将频率视为概率.
(I)若有甲、乙、丙三位顾客选择某种套餐,求三位顾客选择的套餐至少有两样不同的概率;
(II)若用随机变量![]() 表示两位顾客所得优惠金额的综合,求
表示两位顾客所得优惠金额的综合,求![]() 的分布列和期望。
的分布列和期望。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】气象意义上,从春季进入夏季的标志为:“连续5天的日平均温度不低于22℃”.现有甲、乙、丙三地连续5天的日平均温度的记录数据(记录数据都是正整数):
①甲地:5个数据的中位数为24,众数为22;
②乙地:5个数据的中位数为27,总体均值为24;
③丙地:5个数据的中有一个数据是32,总体均值为26,总体方差为10.8;
则肯定进入夏季的地区的有( )
A. ①②③ B. ①③ C. ②③ D. ①
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四边形ABCD中,∠ABC=90°,AC=AD,M,N分别为AC,AD的中点,连接BM,MN,BN.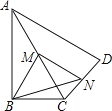
(1)求证:BM=MN;
(2)∠BAD=60°,AC平分∠BAD,AC=2,求BN的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点P的坐标为(x1 , y1),点Q的坐标为(x2 , y2),且x1≠x2 , y1≠y2 , 若P,Q为某个矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为点P,Q的“相关矩形”,如图为点P,Q的“相关矩形”示意图.
(1)已知点A的坐标为(1,0),
①若点B的坐标为(3,1),求点A,B的“相关矩形”的面积;
②点C在直线x=3上,若点A,C的“相关矩形”为正方形,求直线AC的表达式;
(2)⊙O的半径为 ![]() ,点M的坐标为(m,3),若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
,点M的坐标为(m,3),若在⊙O上存在一点N,使得点M,N的“相关矩形”为正方形,求m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA= ![]() acosB. (Ⅰ)求角B的大小;
acosB. (Ⅰ)求角B的大小;
(Ⅱ)若b=3,sinC=2sinA,求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com