练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】过点作互相垂直的直线,,交正半轴于点,交正半轴于点,则线段中点轨迹方程为_______________________;过原点与、、四点的圆半径的最小值为______________.

    【答案】

    【解析】

    设的方程:,则方程为:,求出点,点,即可求得中点轨迹.因为,,所以总存在经过,,,四点的圆,且该圆以为直径,分类讨论,确定、的坐标,表示出,即可求得过原点与、、四点的圆半径的最小值.

    设的方程:,则方程为:

    交正半轴于点,可得

    交正半轴于点,可得

    为线段中点,设

    根据中点坐标公式可得: 即: ,消掉

    线段中点轨迹方程为:

    ,,

    存在经过、、、四点的圆,该圆以为直径．

    ①若轴，轴，

    ②若两条直线斜率均存在，设斜率为

    方程为，

    方程为，

    令，解出

    ，

    ，，

    半径最小值为

    故答案为: ,.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某家庭记录了未使用节水龙头天的日用水量数据（单位：）和使用了节水龙头天的日用水量数据，得到频数分布表如下：

    未使用节水龙头天的日用水量频数分布表

    日用水量

    频数

    使用了节水龙头天的日用水量频数分布表

    日用水量

    频数

    （Ⅰ）作出使用了节水龙头天的日用水量数据的频率分布直方图；

    （Ⅱ）估计该家庭使用节水龙头后，一年能节省多少水？（一年按天计算，同一组中的数据以这组数据所在区间中点的值作代表）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知方程恰有四个不同的实数根，当函数时，实数的取值范围是

    A. B. C. D.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图所示，在四棱锥E-ABCD中，平面ABCD⊥平面AEB，且四边形ABCD为矩形．∠BAE=90°，AE=4，AD=2，F，G，H分别为BE，AE，AD的中点．

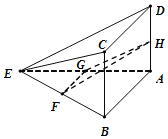
    （Ⅰ）求证：CD∥平面FGH；

    （Ⅱ）求证：平面FGH⊥平面ADE；

    （Ⅲ）在线段DE求一点P，使得AP⊥FH，并求出AP的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的离心率为，右焦点为，左顶点为A，右顶点B在直线上．

    （Ⅰ）求椭圆C的方程；

    （Ⅱ）设点P是椭圆C上异于A，B的点，直线交直线于点，当点运动时，判断以为直径的圆与直线PF的位置关系，并加以证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数是定义在R上的奇函数，当时，则函数＝在上的所有零点之和为

    A. 7 B. 8 C. 9 D. 10

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在口中， ，沿将翻折到的位置，使平面平面.

    （1）求证： 平面；

    （2）若在线段上有一点满足，且二面角的大小为，求的值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知，若方程有2个不同的实根，则实数的取值范围是_____（结果用区间表示）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数（为自然对数的底，为常数，）有两个极值点，且.

    （Ⅰ）求的取值范围；

    （Ⅱ）若恒成立，求实数的取值范围.

    查看答案和解析>>

    同步练习册答案