
 已知an=($\frac{1}{3}$)n,把数列{an}的各项排成如图的三角形,记A(s,t)表示第s行的第t个数,则A(11,12)=( )
已知an=($\frac{1}{3}$)n,把数列{an}的各项排成如图的三角形,记A(s,t)表示第s行的第t个数,则A(11,12)=( )| A. | ($\frac{1}{3}$)67 | B. | ($\frac{1}{3}$)68 | C. | ($\frac{1}{3}$)112 | D. | ($\frac{1}{3}$)113 |
科目:高中数学 来源: 题型:选择题
| A. | $\frac{25}{4}$ | B. | $\frac{31}{4}$ | C. | $\frac{37-6\sqrt{3}}{4}$ | D. | $\frac{37-2\sqrt{33}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=1,g(x)=x0 | B. | f(x)=|x|,g(t)=$\sqrt{{t}^{2}}$ | ||
| C. | f(x)=$\frac{{x}^{2}-1}{x-1}$,g(x)=x+1 | D. | f(x)=lg(x+1)+lg(x-1),g(x)=lg(x2-1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
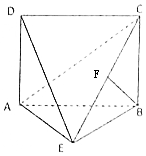 如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.
如图,四边形ABCD为矩形,DA⊥平面ABE,AE=EB=BC=2,BF⊥平面ACE于点F,且点F在CE上.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,$\frac{2\sqrt{6}}{5}$] | B. | [$\frac{\sqrt{3}}{2}$,1) | C. | [$\frac{2\sqrt{6}}{5}$,1) | D. | (0,$\frac{\sqrt{3}}{2}$] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com