
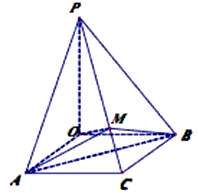
 如图,△BCD中,AB=BC=1,∠ACB=120°,O为△ABC的外心,PO⊥平面ABC,且PO=
如图,△BCD中,AB=BC=1,∠ACB=120°,O为△ABC的外心,PO⊥平面ABC,且PO= .
. (1)证明:连接OC,交AB于点D,O为△ABC的外心,AB=BC=1,OA=OB,OC=0C,故△OAC≌△OBC,∴∠ACO=∠BCO=
(1)证明:连接OC,交AB于点D,O为△ABC的外心,AB=BC=1,OA=OB,OC=0C,故△OAC≌△OBC,∴∠ACO=∠BCO= ∠ACB=60°.
∠ACB=60°. ,OC=1,∴PC=
,OC=1,∴PC= .
. ,建立如图所示的空间坐标系,则得O(0,-
,建立如图所示的空间坐标系,则得O(0,- ,0),A(
,0),A( ,0,0),B(-
,0,0),B(- ,0,0),M(0,
,0,0),M(0, ,
,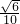 ).
). =(-
=(- ,0,0),
,0,0), =(-
=(- ,
, ,
,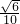 ),
), =(-
=(- ,
, ,0),
,0), =(0,
=(0, ,
,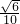 ).
). =(x,y,z),由
=(x,y,z),由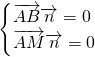 解得
解得 =(0,1,-
=(0,1,- ).
). =(x′,y′,z′),由
=(x′,y′,z′),由 解得
解得 =(1,
=(1, ,-4
,-4 ).
). ,
, >=
>= =
=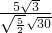 =
=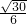 ,故sin<
,故sin< ,
, >=
>= ,故二面角A-BM-O的正弦值为
,故二面角A-BM-O的正弦值为 .
. 和
和 的坐标,利用两个向量的夹角公式求出cos<
的坐标,利用两个向量的夹角公式求出cos< ,
, >,从而求出sin<
>,从而求出sin< ,
, >的值,即得所求
>的值,即得所求

 寒假乐园北京教育出版社系列答案
寒假乐园北京教育出版社系列答案科目:高中数学 来源: 题型:
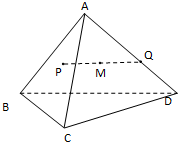 如图,在三棱锥A-BCD中,AB,AC,AD两两互相垂直,AB=AC=AD=4,点P,Q分别在侧面ABC棱AD上运动,PQ=2,M为线段PQ中点,当P,Q运动时,点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于
如图,在三棱锥A-BCD中,AB,AC,AD两两互相垂直,AB=AC=AD=4,点P,Q分别在侧面ABC棱AD上运动,PQ=2,M为线段PQ中点,当P,Q运动时,点M的轨迹把三棱锥A-BCD分成上、下两部分的体积之比等于查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
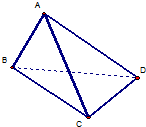 如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=
如图,在三棱锥A-BCD中,侧面ABD、ACD是全等的直角三角形,AD是公共的斜边,且AD=| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com