
解:取物体运动的起点为原点,在t时刻的位移为s=s(t),速度为v=v(t),加速度为a=a(t),则有s′(t)=v(t),v′(t)=a(t)=2![]() +1,?s(0)=0,v(0)=1.?
+1,?s(0)=0,v(0)=1.?
在时间[0,t]上有?
v(t)-v(0)=∫![]() a(t)dt=∫
a(t)dt=∫![]() (2
(2![]() +1)dt?
+1)dt?
=(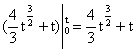 ,?
,?
∴v(t)=![]() +t+1.?
+t+1.?
s(t)-s(0)=![]() ?
?
=(![]() ·
·![]()
![]() +
+![]() t2+t)
t2+t)![]()
=![]() +
+![]() t2+t.?
t2+t.?
∵s(0)=0,?
∴s(t)= ![]() +
+![]() t2+t,t∈[0,+∞).?
t2+t,t∈[0,+∞).?
温馨提示:物体做变速直线运动的速度v,等于加速度函数a=a(t)在时间区间[a,b]上的定积分![]() ;物体做变速直线运动经过的路程s,等于其速度函数v=v(t)[v(t)≥0]在时间区间[a,b]上的定积分
;物体做变速直线运动经过的路程s,等于其速度函数v=v(t)[v(t)≥0]在时间区间[a,b]上的定积分![]() .
.


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com