
.(本小题10分)
在一次购物抽奖活动中,假设某10张券中有一等奖券1张,可获价值50元的奖品;有二等奖券3张,每张可获价值10元的奖品;其余6张没有奖,某顾客从此10张券中任抽2张,求:(1)该顾客中奖的概率;(2)该顾客获得的奖品总价值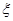 (元)的概率分布列和期望
(元)的概率分布列和期望 .
.
(1) (2)由于10张券总价值为80元,即每张的平均奖品价值为8元,从而抽2张的平均奖品价值
(2)由于10张券总价值为80元,即每张的平均奖品价值为8元,从而抽2张的平均奖品价值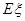 =2×8=16(元).
=2×8=16(元).
【解析】本题考查等可能事件的概率和互斥事件的概率,本题解题的关键是看出要求概率的事件包含的结果数比较多,注意做到不重不漏.
(1)本题是一个等可能事件的概率,而顾客中奖的对立事件是顾客不中奖,从10张中抽2张有C102种结果,抽到的不中奖有C62种结果,得到概率
(2) 的所有可能值为:0,10,20,50,60(元)然后接合古典概型得到概率值,求解分布列。.
的所有可能值为:0,10,20,50,60(元)然后接合古典概型得到概率值,求解分布列。.
解法一:
(1)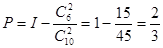 ,即该顾客中奖的概率为
,即该顾客中奖的概率为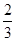 . -----------3分
. -----------3分
(2) 的所有可能值为:0,10,20,50,60(元).
-----------4分
的所有可能值为:0,10,20,50,60(元).
-----------4分
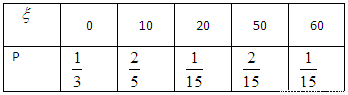
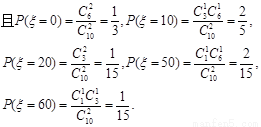 -----------7分
-----------7分
故 有分布列:----------9分
有分布列:----------9分
从而期望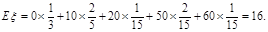 ----------10分
----------10分
解法二:
(1) (2)
(2) 的分布列求法同解法一
的分布列求法同解法一
由于10张券总价值为80元,即每张的平均奖品价值为8元,从而抽2张的平均奖品价值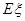 =2×8=16(元).
=2×8=16(元).


 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:高中数学 来源: 题型:
| 3 |
查看答案和解析>>
科目:高中数学 来源:2010年浙江省杭州市七校高二上学期期中考试数学文卷 题型:解答题
(本小题10分)
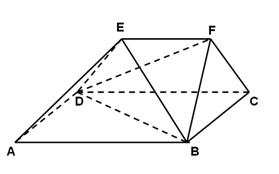
如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC.
(1)求证:平面ABFE⊥平面DCFE;
(2)求四面体B—DEF的体积.
查看答案和解析>>
科目:高中数学 来源:2010年哈尔滨三中高一下学期第二模块数学卷 题型:解答题
(本小题10分)
棱长为2的正方体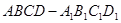 中,
中,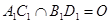 .
.
①求异面直线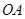 与
与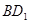 所成角的余弦值;
所成角的余弦值;
②求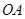 与平面
与平面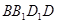 所成角的余弦值.
所成角的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com