
|
| A、[1,5] |
| B、[2,6] |
| C、[3,10] |
| D、[3,11] |
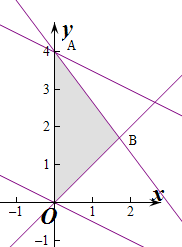 解:作出不等式组对应的平面区域如图:(阴影部分).
解:作出不等式组对应的平面区域如图:(阴影部分).| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| A、存在四边相等的四边形不是正方形 |
| B、z1,z2∈C,z1+z2为实数的充分必要条件是z1,z2为共轭复数 |
| C、若x,y∈R,且x+y>2则x,y至少有一个大于1 |
| D、命题:?n∈N,2n>1000的否定是:?n∈N,2n≤1000 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
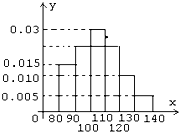 某校高一某班共有64名学生,如图是该班某次数学考试成绩的频率分布直方图,根据该图可知,成绩在110-120间的同学大约有( )
某校高一某班共有64名学生,如图是该班某次数学考试成绩的频率分布直方图,根据该图可知,成绩在110-120间的同学大约有( )| A、10 | B、11 | C、13 | D、16 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com