Question

19．已知集合M是满足下列条件的函数f（x）的全体：存在非零常数T，对任意x∈R，有f（x+T）=Tf（x）成立．给出如下函数：①f（x）=x；②f（x）=2^x；③f（x）=$\frac{1}{2^x}$；④f（x）=x²；则属于集合M的函数个数为（　　）

• A． 1
• B． 2
• C． 3
• D． 4

Answer 1

分析 根据条件定义分别验证有f（x+T）=Tf（x）是否恒成立即可．

解答 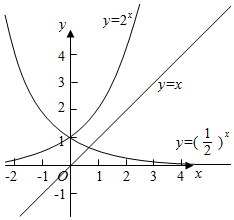解：①若f（x）=x，
则f（x+T）=x+T，Tf（x）=Tx，
∴x+T=Tx，不可能成立，不存在非零常数T，使f（x+T）=Tf（x）成立，则①不属于集合M的函数；
②f（x）=2^x；
则f（x+T）=2^x+T=2^T•2^x，
由f（x+T）=Tf（x）得2^T•2^x=T•2^x，
即2^T=T，
作出函数y=2^x和y=x的图象，由图象知两个函数没有交点，
即方程2^T=T无解，
∴不存在非零常数T，使f（x+T）=Tf（x）成立，则②不属于集合M的函数；
③若f（x）=$\frac{1}{2^x}$
则f（x+T）=（$\frac{1}{2}$）^x+T=（$\frac{1}{2}$）^T•（$\frac{1}{2}$）^x，
由f（x+T）=Tf（x）得（$\frac{1}{2}$）^T•（$\frac{1}{2}$）^x=T•（$\frac{1}{2}$）^x，
即（$\frac{1}{2}$）^T=T，
作出函数y=（$\frac{1}{2}$）^x和y=x的图象，由图象知两个函数有1个交点，
即方程（$\frac{1}{2}$）^T=T有一个解，
∴存在非零常数T，使f（x+T）=Tf（x）成立，则③属于集合M的函数；
④f（x）=x²；
则f（x+T）=（x+T）²，
由f（x+T）=Tf（x）得（x+T）²=T•x²，
即x²+2xT+T²=T•x²，
则方程x²+2xT+T²=T•x²，不可能恒成立，
∴不存在非零常数T，使f（x+T）=Tf（x）成立，则④不属于集合M的函数．
故选：A．

点评 本题主要考查函数恒成立问题，根据抽象函数的关系分别进行验证是解决本题的关键．