解:(1)由程序框图所给的算法可知y是关于随机变量x的函数.
当x<5时,由不等式2
x-8<0可得x<3,故x可取1,2;
当5≤x≤10时,由不等式x
2-14x+45<0可得5<x<9,故x可取6,7,8;
,从{1,2,3,…,10}中随机地抽出一个数x,基本事件的总数为10,
事件y<0包含的基本事件的个数为5,
由古典概型的概率公式得n=10时,y<0的概率为
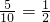
;
(2)当x<5时,由不等式2
x-8>0可得x>3,故x可取4;
当x≥5时,由不等式x
2-14x+45>0可得x>9;
所以当n<4时,p(y>0)=0;
当4≤n<10时,p(y>0)=

,

;
当n≥10时,p(y>0)=
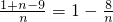
,

.
由P(y>0)=

知4≤n<10,由

得n=6.
当x分别取1,2,3,4,5,6时,输出的y值依次为-6,-4,0,8,0,-3,
故ξ的分布列为

Eξ=-6×
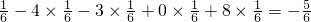
分析:(1)由程序框图所给的算法可知y是关于变量x的分段函数,通过解不等式求出y<0包含的基本事件的个数为5,利用古典概型的概率公式求出n=10时,y<0的概率.
(2)求出y>0时,x可取的值,通过对n的讨论求出P(y>0)的范围,根据已知条件P(y>0)=

,求出n的值,求出
ξ的所有取值,并求出取各值的概率值,列出分布列,求出期望.
点评:本题考查离散型随机变量的分布列和期望,考查等可能事件的概率,考查分类讨论的数学思想方法,是一个综合题,是近几年高考题目中经常出现的一个问题.

 从{1,2,3,…,n}中随机地抽出一个数x,按右边程序框图所给算法输出y.
从{1,2,3,…,n}中随机地抽出一个数x,按右边程序框图所给算法输出y. ,记输出的y值为ξ,求ξ的分布列和数学期望.
,记输出的y值为ξ,求ξ的分布列和数学期望.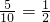 ;
; ,
, ;
;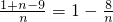 ,
, .
. 知4≤n<10,由
知4≤n<10,由 得n=6.
得n=6.
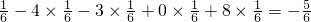
 ,求出n的值,求出
,求出n的值,求出

 阅读快车系列答案
阅读快车系列答案