
某人在塔的正东沿着南偏西60°的方向前进40米后,望见塔在东北方向,若沿途测得塔的最大仰角为30°,求塔高.
解:
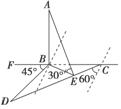
依题意画出图,某人在C处,AB为塔高,他沿CD前进,CD=40米,此时∠DBF=45°,从C到D沿途测塔的仰角,只有B到测试点的距离最短时,仰角才最大,这是因为tan∠AEB=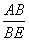 ,AB为定值,BE最小时,仰角最大.要求出塔高AB,必须先求BE,而要求BE,需先求BD(或BC).
,AB为定值,BE最小时,仰角最大.要求出塔高AB,必须先求BE,而要求BE,需先求BD(或BC).
在△BCD中,CD=40,∠BCD=30°,∠DBC=135°.
由正弦定理,得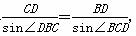
∴BD= =20
=20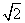 .
.
在Rt△BED中,∠BDE=180°-135°-30°=15°,
BE=BDsin15°=20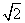 ×
×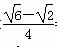 =10(
=10(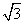 -1)(米).
-1)(米).
在Rt△ABE中,∠AEB=30°,
∴AB=BEtan30°=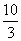 (3-
(3-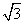 )(米).
)(米).
∴所求的塔高为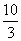 (3-
(3-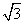 )米.
)米.


科目:高中数学 来源: 题型:
已知函数f(x)=Asin(ωx+φ),x∈R,(其中A>0,ω>0,0<φ<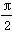 )的图象与x轴的交点中,相邻两个交点之间的距离为
)的图象与x轴的交点中,相邻两个交点之间的距离为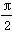 ,且图象上的一个最低点为M
,且图象上的一个最低点为M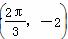 .
.
(1)求 f(x)的解析式;
f(x)的解析式;
(2)当x∈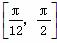 时,求f(x)的值域.
时,求f(x)的值域.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知A 、B两地间的距离为10 km,B、C两地间的距离为20 km,现测得∠ABC=120°,则A、C两地间的距离为( )
、B两地间的距离为10 km,B、C两地间的距离为20 km,现测得∠ABC=120°,则A、C两地间的距离为( )
A.10 km B.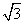 km
km
C.10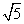 km D.10
km D.10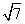 km
km
查看答案和解析>>
科目:高中数学 来源: 题型:
“温馨花园”为了美化小区,给居民提供更好的生活环境,在小区内如图的一块三角形空地上种植草皮(单位:m),已知这种草皮的价格是120元/m2,则购买这种草皮需要________元.
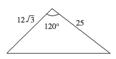
查看答案和解析>>
科目:高中数学 来源: 题型:
数列{an}的通项公式是关于x的不等式x2-x<nx(n∈N*)的解集中的整数个数,则数列{an}的前n项和Sn=( )
A.n2 B.n(n+1)
C. 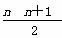 D.(n+1)(n+2)
D.(n+1)(n+2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com